Question

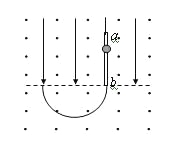
【题目】如图所示，在O处固定一个电荷量为Q=+1.0×10-9C的点电荷，现用长L=0.2m的绝缘细线拴一个质量m=0.06kg的带电小球(可视为点电荷) 后也悬挂于O处，细线所受拉力达到F=6mg时就会被拉断。将小球拉至与悬点O等高，并且使细线伸直，然后由静止释放，当悬线转过90°到到达B位置时，细线恰好拉断。之后小球将从B点进入板间距d=0.08m的两平行板电容器，并恰好沿水平方向做匀速直线运动(进入电容器后不考虑O处点电荷对小球的作用力)，且此时电路中的电动机刚好能正常工作。已知电源的电动势为12V，内阻1Ω，定值电阻、、的阻值均为6Ω，电动机的内阻为1Ω。忽略空气阻力和电容器的边缘效应，取g=10m/s2，静电力常量k=9.0×109N·m2/C2。求：

（1）小球到达B 点时的速度大小；

（2）小球所带的电荷量；

（3）电动机的机械功率。

Answer 1

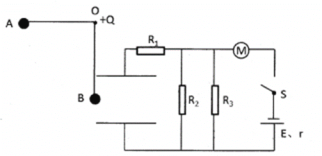
【答案】（1）小球到达B点时的速度为2m/s；
（2）小球所带的电荷量为8×10-3C；
（3）电动机的机械功率为4.0W。

【解析】

（1）由机械能守恒得：

代入数据解得：

vB=2m/s

（2）到达B点绳恰好作用力为6mg，由牛顿第二定律得：

代入数据解得：

q=8×10-3C

（3）设电容器两端电压为U，由二力平衡得：

①

由欧姆定律得：

②

所以，电动机两端电压：

UM=E-U-Ir③

P机=P总-P热=IUM-I2rM④

联立①②③④解得：

P机=4.0W