��Ŀ����
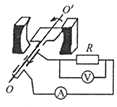
����Ŀ����ͼ��ʾ����x���Ϸ����ڴ�ֱ��ֽ���������ǿ�ų����Ÿ�Ӧǿ��ΪB��ԭ��O������һ����Դ����ͬʱ�����������Ϊm�������Ϊq�Ĵ��������ӣ��������ƣ����ٶȷ������xOyƽ���ڣ���x��������ļнǦ���0��180�㷶Χ�ڣ�������˵����ȷ���ǣ� ��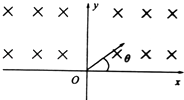
A.�����ٶȴ�С��ͬ�����ӣ���Խ��������ڴų����˶���ʱ��Խ��
B.�����ٶȴ�С��ͬ�����ӣ���Խ��������뿪�ų�ʱ��λ�þ�O��ԽԶ
C.����ǶȦ���ͬ�����ӣ��ٶ�Խ��������ڴų����˶���ʱ��Խ��
D.����ǶȦ���ͬ�����ӣ��ٶ�Խ��������ڴų����˶��Ľ��ٶ�Խ��
���𰸡�A
���������⣺A���ٶ���ͬ�������ڴų��а뾶��ͬ�����������ڴų����˶��Ĺ켣��ͼ��ʾ��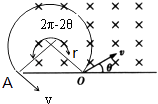
�ɼ��ι�ϵ�ã��켣��Ӧ��Բ�ĽǦ�=2�Щ�2�ȣ������ڴų����˶���ʱ��t= ![]() T=
T= ![]()
![]() =
= ![]() �����֪����Խ��ʱ��tԽ�̣�����һ�����˶�ʱ��һ������A��ȷ��C����
�����֪����Խ��ʱ��tԽ�̣�����һ�����˶�ʱ��һ������A��ȷ��C����
B�������ӵĹ켣�뾶Ϊr����r= ![]() ����ͼ��AO=2rsin��=
����ͼ��AO=2rsin��= ![]() ������������ǣ���Խ��AOԽ�������Ƕ۽ǣ���Խ��AOԽС����B����
������������ǣ���Խ��AOԽ�������Ƕ۽ǣ���Խ��AOԽС����B����
D�������ڴų����˶��Ľ��ٶȦ�= ![]() ����T=
����T= ![]() ����æ�=
����æ�= ![]() �����ٶ�v�ͽǶ��أ���D����
�����ٶ�v�ͽǶ��أ���D����
��ѡ��A��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�