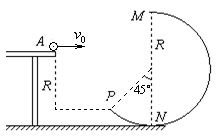
题目内容
如图所示,斜面倾角为θ,斜面上AB段光滑,其它部分粗糙,且斜面足够长。一带有速度传感器的小物块(可视为质点),自A点由静止开始沿斜面下滑,速度传感器上显示的速度与运动时间的关系如下表所示:
取g=10m/s2,求:
(1)斜面的倾角θ多大?
(2)小物块与斜面的粗糙部分间的动摩擦因数μ为多少?
(3)AB间的距离xAB等于多少?
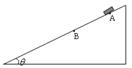
| 时间(s) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | …. |
| 速度(m/s) | 0 | 6 | 12 | 17 | 21 | 25 | 29 | …… |
取g=10m/s2,求:
(1)斜面的倾角θ多大?
(2)小物块与斜面的粗糙部分间的动摩擦因数μ为多少?
(3)AB间的距离xAB等于多少?

(1)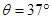 (2)
(2)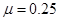 (3)18.75m
(3)18.75m
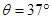 (2)
(2)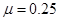 (3)18.75m
(3)18.75m试题分析:(1)当小物块在AB段运动时,设加速度为
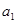 ,根据牛顿第二定律
,根据牛顿第二定律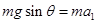 得
得 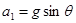 (2分)
(2分)由表格可知
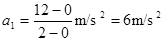
所以
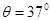
(2)过B点后物块的加速度设为
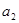 ,根据牛顿第二定律
,根据牛顿第二定律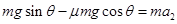 得
得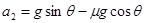 (2分)
(2分)由表格可知
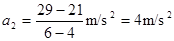
所以
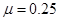
(3)可以判断B点对应于2s~3s之间的某个时刻,设
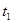 为从第2s时刻运动至B点所用时间,
为从第2s时刻运动至B点所用时间,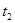 为从B点运动至第3s时刻所用时间。
为从B点运动至第3s时刻所用时间。则
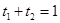 s
s 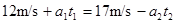
解之得
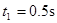
所以
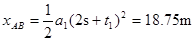
点评:中等难度。本题根据表格中的数据算出加速度,然后在由牛顿第二定律求出所需物理量,属于牛顿第二定律应用的典型习题。

练习册系列答案
相关题目

 ;
;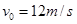 的速度匀速行驶,其所受阻力可视为与车重成正比,与速度无关。某时刻,车厢脱落,并以大小为
的速度匀速行驶,其所受阻力可视为与车重成正比,与速度无关。某时刻,车厢脱落,并以大小为 的加速度减速滑行。在车厢脱落
的加速度减速滑行。在车厢脱落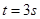 后,司机才发觉并紧急刹车,刹车时阻力为正常行驶时的3倍。假设刹车前牵引力不变,求卡车和车厢都停下后两者之间的距离。
后,司机才发觉并紧急刹车,刹车时阻力为正常行驶时的3倍。假设刹车前牵引力不变,求卡车和车厢都停下后两者之间的距离。