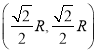题目内容
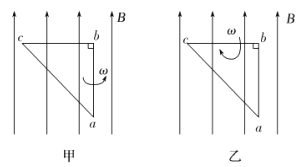
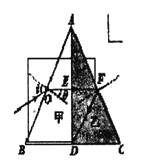
【题目】由两种不同透明介质制成的直角三棱镜甲和乙,并排放在一起刚好构成一截面为正三角形的棱镜,甲的折射率为![]() ,一细光束由AB边的中点0斜射入棱镜甲,已知入射光线在AB边的入射角的正弦值为
,一细光束由AB边的中点0斜射入棱镜甲,已知入射光线在AB边的入射角的正弦值为![]() ,经折射后该光束刚好在棱镜乙的AC边发生全反射,最后从BC边射出,已知真空中的光速为
,经折射后该光束刚好在棱镜乙的AC边发生全反射,最后从BC边射出,已知真空中的光速为![]() ,AB边的长度为
,AB边的长度为![]() ,求该细光束在棱镜中的传播时间。
,求该细光束在棱镜中的传播时间。

【答案】![]()
【解析】解:由题意可知该细光束在棱镜甲中的传播速度为:![]()
设该细光束在AB边的折射角为![]() ,由折射定律可得:
,由折射定律可得:![]() ,得到:
,得到:![]()
由几何关系可知,细光束在棱镜中的折射光线与AB边的夹角为![]() ,故折射光与底边BC平行,光线进入棱镜乙时传播方向不变。
,故折射光与底边BC平行,光线进入棱镜乙时传播方向不变。
因光线刚好在AC边发生全反射,由几何知识得到,光线在AC边的入射角为![]() ,即临界角为:
,即临界角为:![]()
设棱镜乙的折射率为![]() ,则有
,则有![]() ,得到:
,得到:![]()
则该细光束在棱镜乙中的传播速度为![]()
由几何关系可知:![]() ,
,![]() ,
,![]()
则该光束在棱镜中的传播时间为:![]() 。
。

练习册系列答案
相关题目
【题目】某十字路口的监控录像显示,一辆汽车在马路上行驶,t=0时,汽车在十字路口中心的左侧20m处;过了2s,汽车正好到达十字路口的中心;再过3s,汽车行驶到了十字路口中心右侧30m处.如果把这条马路抽象为一条坐标轴x,十字路口中心定为坐标轴的原点,向右为x轴的正方向.

(1)试将汽车在三个观测时刻的位置坐标填入表中.
观测 时刻 | t=0时 | 过2s | 再过3s |
位置 坐标 | x1= | x2= | x3= |
(2)说出前2s内、后3s内汽车的位移分别为多少?这5s内的位移又是多少?