题目内容
4.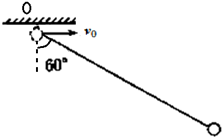 如图所示,长为l 的轻绳一端系于固定点O,另一端系一质量为m的小球.将小球从O点处以一定的初速度水平向右抛出,经一定的时间,绳被拉直,以后小球将以O为圆心在竖直平面内摆动.已知绳刚被拉直时,绳与竖直线成60°角,则小球水平抛出的初速度v0=$\frac{\sqrt{3gl}}{2}$.(不计一切阻力,已知重力加速度为g)
如图所示,长为l 的轻绳一端系于固定点O,另一端系一质量为m的小球.将小球从O点处以一定的初速度水平向右抛出,经一定的时间,绳被拉直,以后小球将以O为圆心在竖直平面内摆动.已知绳刚被拉直时,绳与竖直线成60°角,则小球水平抛出的初速度v0=$\frac{\sqrt{3gl}}{2}$.(不计一切阻力,已知重力加速度为g)
分析 平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,根据高度求出时间,再根据水平位移和时间求出平抛运动的初速度.
解答 解:(1)小球在绳被拉直前作平抛运动,设小球抛出后经时间t绳被拉直,则:
水平位移为:lsin60°=v0t.
竖直高度为:lcos60°=$\frac{1}{2}g{t}^{2}$
解得:${v}_{0}=\frac{\sqrt{3gl}}{2}$
故答案为:$\frac{\sqrt{3gl}}{2}$
点评 本题综合考查了平抛运动和圆周运动,关键掌握平抛运动在水平方向和竖直方向上的运动规律,难度不大,属于基础题.

练习册系列答案
相关题目
19.在学校运动会上,刘伟在男子100m决赛和男子200m决赛中分别以11.80s和24.60s的成绩获得两枚金牌.关于他在这两次决赛中的运动情况,下列说法正确的是( )
| A. | 200 m决赛中的位移是100 m决赛的两倍 | |
| B. | 200 m决赛中的平均速度约为8.13m/s | |
| C. | 100 m决赛中的平均速度约为8.47m/s | |
| D. | 100 m决赛中的中间时刻的速度约为8.47m/s |
9.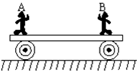 如图所示,一辆小车静止在光滑水平面上,A、B两人分别站在车的两端,当两人同时相向运动时( )
如图所示,一辆小车静止在光滑水平面上,A、B两人分别站在车的两端,当两人同时相向运动时( )
 如图所示,一辆小车静止在光滑水平面上,A、B两人分别站在车的两端,当两人同时相向运动时( )
如图所示,一辆小车静止在光滑水平面上,A、B两人分别站在车的两端,当两人同时相向运动时( )| A. | 若小车不动,两人速率一定相等 | |
| B. | 若小车向左运动,A的速率一定比B的小 | |
| C. | 若小车向左运动,A的动量一定比B的大 | |
| D. | 若小车向左运动,A的动量一定比B的小 |
16.如图所示,在一光滑水平面上放一个物体,人通过细绳跨过高处的定滑轮拉物体,使物体在水平面上运动,人以大小不变的速度v运动.当绳子与水平方向成θ角时,物体前进的瞬时速率是( )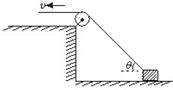

| A. | vcosθ | B. | $\frac{v}{cosθ}$ | C. | vsinθ | D. | $\frac{v}{sinθ}$ |
13.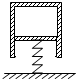 如图所示,竖直的弹簧支持着一倒立气缸内的活塞,使气缸悬空而静止.设活塞与缸壁间无摩擦,可以在缸内自由移动.缸壁导热性良好,缸内气体的温度能与外界大气温度相同.下列结论中正确的是( )
如图所示,竖直的弹簧支持着一倒立气缸内的活塞,使气缸悬空而静止.设活塞与缸壁间无摩擦,可以在缸内自由移动.缸壁导热性良好,缸内气体的温度能与外界大气温度相同.下列结论中正确的是( )
 如图所示,竖直的弹簧支持着一倒立气缸内的活塞,使气缸悬空而静止.设活塞与缸壁间无摩擦,可以在缸内自由移动.缸壁导热性良好,缸内气体的温度能与外界大气温度相同.下列结论中正确的是( )
如图所示,竖直的弹簧支持着一倒立气缸内的活塞,使气缸悬空而静止.设活塞与缸壁间无摩擦,可以在缸内自由移动.缸壁导热性良好,缸内气体的温度能与外界大气温度相同.下列结论中正确的是( )| A. | 若外界大气压减小,则弹簧的压缩量将会减小一些 | |
| B. | 若外界大气压减小,则弹簧的压缩量将会增大一些 | |
| C. | 若外界气温升高,则气缸的上底面距地面的高度将增大 | |
| D. | 若外界气温升高,则气缸的上底面距地面的高度将减小 |
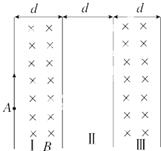 如图所示,一个带负电的粒子沿磁场边界从A点射出,粒子质量为m、电荷量为-q,其中区域Ⅰ、Ⅲ内的匀强磁场宽为d,磁感应强度为B,区域Ⅱ宽也为d,粒子从A点射出后经过Ⅰ、Ⅱ、Ⅲ区域后能回到A点,不计粒子重力.
如图所示,一个带负电的粒子沿磁场边界从A点射出,粒子质量为m、电荷量为-q,其中区域Ⅰ、Ⅲ内的匀强磁场宽为d,磁感应强度为B,区域Ⅱ宽也为d,粒子从A点射出后经过Ⅰ、Ⅱ、Ⅲ区域后能回到A点,不计粒子重力. 如图,高台的上面有一竖直的$\frac{1}{4}$圆弧形光滑轨道,半径R=$\frac{5}{4}$m,轨道端点B的切线水平.质量M=5kg的金属滑块(可视为质点)由轨道顶端A由静止释放,离开B点后经时间t=1s撞击在斜面上的P点.已知斜面的倾角θ=37°,斜面底端C与B点的水平距离x0=3m.g取10m/s2,sin37°=0.6,cos37°=0.8,不计空气阻力.
如图,高台的上面有一竖直的$\frac{1}{4}$圆弧形光滑轨道,半径R=$\frac{5}{4}$m,轨道端点B的切线水平.质量M=5kg的金属滑块(可视为质点)由轨道顶端A由静止释放,离开B点后经时间t=1s撞击在斜面上的P点.已知斜面的倾角θ=37°,斜面底端C与B点的水平距离x0=3m.g取10m/s2,sin37°=0.6,cos37°=0.8,不计空气阻力.
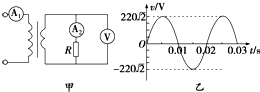 如图甲所示,调压器装置可视为理想变压器,负载电路中R=55Ω,A、V 为理想电流表和电压表,电压表的示数为110V,若原线圈接入如图乙所示的正弦交变电压,则:电流表A2的示数为2A,A1的示数为1A,原线圈中电流的瞬时值表达式为:i=$\sqrt{2}sin100πt$(A).
如图甲所示,调压器装置可视为理想变压器,负载电路中R=55Ω,A、V 为理想电流表和电压表,电压表的示数为110V,若原线圈接入如图乙所示的正弦交变电压,则:电流表A2的示数为2A,A1的示数为1A,原线圈中电流的瞬时值表达式为:i=$\sqrt{2}sin100πt$(A).