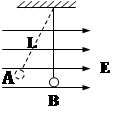题目内容
(15分)如图所示,在竖直平面内有范围足够大、水平向左的匀强电场。一绝缘U形弯杆由两段直杆和一半径为R的半圆环MAP组成,固定在纸面所在的竖直平面内。PQ、MN水平且足够长,NMAP段是光滑的。现有一质量为m、带电量为+q的小环套在MN杆上,它所受电场力为重力的3/4(重力加速度为g)。现在M右侧D点由静止释放小环,小环刚好能到达P点。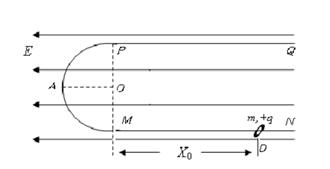
(1)求D、M间的距离X0;
(2)求上述过程中小环第一次通过与O等高的A点时弯杆对小环作用力的大小;
(3)若小环与PQ间动摩擦因数为μ(设最大静摩擦力与动摩擦力大小相等且大于电场力),现将小环移至M点右侧4R处由静止开始释放,球小环在整个运动过程中克服摩擦力所做的功。
⑴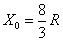 ⑵
⑵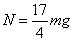 ⑶
⑶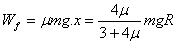
解析试题分析:(1)(5分)从D点到P点,由动能定理得: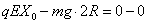
得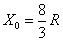
(2)(5分)从P到A点,由动能定理得: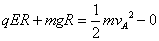
在A点,由牛顿第二定律得: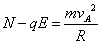 得:
得: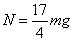
(3)(5分)从M点右侧4R处释放,到达P点: 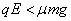 ,
,
小球到达P点后向右运动位移x后速度为零,
根据动能定理有:qE 4R-mg2R-qE x-µmg.x=0-0
所以克服摩擦力所做的功为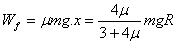
考点:本题考查动能定理。

练习册系列答案
相关题目
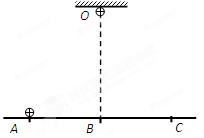
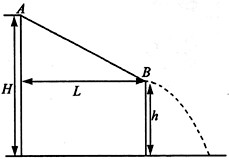
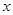 的A点,用水平恒力将质量为m的质点从静止开始推到B处后撤去恒力,然后沿半圆轨道运动到C处后,又正好落回到A点,求:
的A点,用水平恒力将质量为m的质点从静止开始推到B处后撤去恒力,然后沿半圆轨道运动到C处后,又正好落回到A点,求:
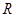 、
、 表示);
表示);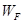 与
与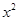 的关系如图所示,试求小球的质量和圆轨道半径。(
的关系如图所示,试求小球的质量和圆轨道半径。(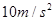 )
)