题目内容
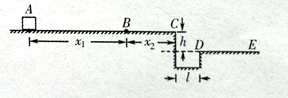
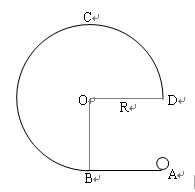
如图所示,固定斜面AB、CD与竖直光滑圆弧BC相切于B、C点,两斜面的倾角θ=37°,圆弧BC半径R=2m。一质量m="1" kg的小滑块(视为质点)从斜面AB上的P点由静止沿斜面下滑,经圆弧BC冲上斜面CD。已知P点与斜面底端B间的距离L1="6" m,滑块与两斜面间的动摩擦因数均为μ=0.25,g=10m/s2。求;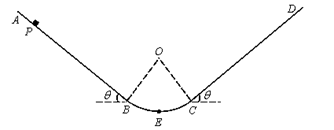
(1)小滑块第1次经过圆弧最低点E时对圆弧轨道的压力;
(2)小滑块第1次滑上斜面CD时能够到达的最远点Q(图中未标出)距C点的距离;
(1)50 N 方向竖直向下(2)3 m
解析试题分析:(1)小滑块由P运动到E点,根据动能定理有:
在E点的向心力:
解得:FN="50" N。
滑块对轨道的压力: ,方向竖直向下
,方向竖直向下
(2)设小滑块在斜面AB上依次下滑的距离分别为L1、L2、L3……在斜面CD上依次上滑的距离分别为x1、x2、x3……
小滑块由P运动到Q点,根据动能定理有: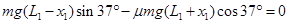
解得: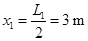
考点:本题考查动能定理,涉及圆周运动和多过程问题。

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
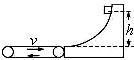
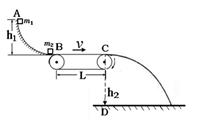
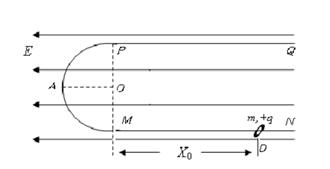
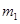 的滑块(可视为质点)自光滑圆弧形槽的顶端A处无初速度的滑下。槽的底端与水平传送带相切于左传导轮顶端的B点,A、B的高度差为
的滑块(可视为质点)自光滑圆弧形槽的顶端A处无初速度的滑下。槽的底端与水平传送带相切于左传导轮顶端的B点,A、B的高度差为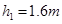 .传导轮半径很小,两个轮之间的距离为
.传导轮半径很小,两个轮之间的距离为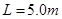 ,滑块与传送带间的动摩擦因数
,滑块与传送带间的动摩擦因数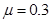 .右端的轮子上沿距离地面的高度为
.右端的轮子上沿距离地面的高度为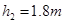 .(
.(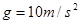 )
)
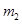 ,传送带静止不转,滑块
,传送带静止不转,滑块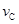 ;
;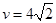 m/s。求滑块
m/s。求滑块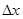 。
。
 m/s平抛救生圈,第一个刚落到快艇上时,紧接着抛第二个,结果第二个救生圈刚好与甲队员同时抵达快艇上的同一位置,取g=10m/s2,不计空气阻力,求:
m/s平抛救生圈,第一个刚落到快艇上时,紧接着抛第二个,结果第二个救生圈刚好与甲队员同时抵达快艇上的同一位置,取g=10m/s2,不计空气阻力,求: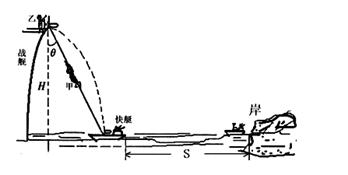
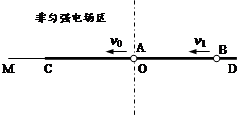
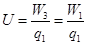
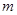 ,从离桌面高为
,从离桌面高为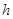 处由静止释放,假设它与桌面碰撞反弹时不损失机械能,但由于受到大小不变的空气阻力的影响(空气浮力不计),每次反弹的高度是它下落时高度的
处由静止释放,假设它与桌面碰撞反弹时不损失机械能,但由于受到大小不变的空气阻力的影响(空气浮力不计),每次反弹的高度是它下落时高度的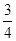 。求:
。求: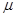 =0.2,取g=10m/s2,求:
=0.2,取g=10m/s2,求: