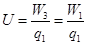题目内容
(18分)如图所示,光滑水平面右端B处连接一个竖直的半径为R的光滑圆轨道,在离B距离为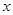 的A点,用水平恒力将质量为m的质点从静止开始推到B处后撤去恒力,然后沿半圆轨道运动到C处后,又正好落回到A点,求:
的A点,用水平恒力将质量为m的质点从静止开始推到B处后撤去恒力,然后沿半圆轨道运动到C处后,又正好落回到A点,求: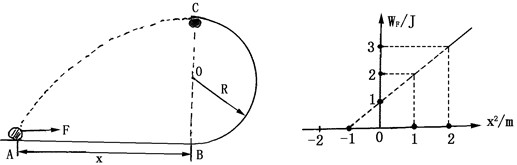
(1)试推导小球在C点飞出时的速度表达式(用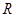 、
、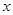 、
、 表示);
表示);
(2)欲完成上述运动,当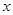 为何值时推力做的功最小?最小值为多少?
为何值时推力做的功最小?最小值为多少?
(3)若水平恒力做的功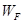 与
与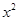 的关系如图所示,试求小球的质量和圆轨道半径。(
的关系如图所示,试求小球的质量和圆轨道半径。( 取
取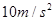 )
)
(1)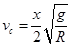 ,(2)
,(2)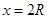 时,推力做功最小为
时,推力做功最小为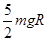 (3)
(3)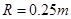 ,
,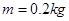
解析试题分析: (1)离开C点后作平抛运动: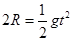 ① (2分)
① (2分)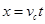 ② (2分)
② (2分)
解得: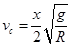 ③ (1分)
③ (1分)
(2)A→C由动能定理: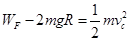 ④ (2分)
④ (2分)
可得: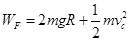
而欲完成圆周运动,需最高点: 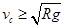 ⑤ (2分)
⑤ (2分)
由③⑤得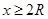 ,
, 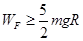 (1分)
(1分)
则当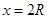 时,推力做功最小为
时,推力做功最小为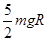 (2分)
(2分)
(3)由③④得: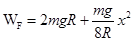 ⑥ (2分)
⑥ (2分)
由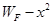 图可得:斜率为
图可得:斜率为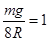 ⑦ (1分)
⑦ (1分)
纵截距为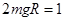 ⑧ (1分)
⑧ (1分)
由⑦⑧得: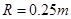 (1分)
(1分)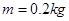 (1分)
(1分)
考点:本题考查了平抛运动、圆周运动规律、动能定理、图象的认识和处理。

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目


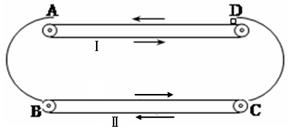
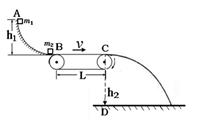
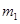 的滑块(可视为质点)自光滑圆弧形槽的顶端A处无初速度的滑下。槽的底端与水平传送带相切于左传导轮顶端的B点,A、B的高度差为
的滑块(可视为质点)自光滑圆弧形槽的顶端A处无初速度的滑下。槽的底端与水平传送带相切于左传导轮顶端的B点,A、B的高度差为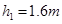 .传导轮半径很小,两个轮之间的距离为
.传导轮半径很小,两个轮之间的距离为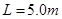 ,滑块与传送带间的动摩擦因数
,滑块与传送带间的动摩擦因数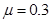 .右端的轮子上沿距离地面的高度为
.右端的轮子上沿距离地面的高度为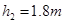 .(
.(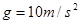 )
)
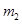 ,传送带静止不转,滑块
,传送带静止不转,滑块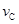 ;
;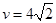 m/s。求滑块
m/s。求滑块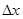 。
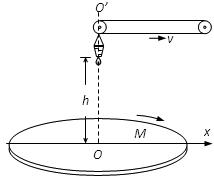
。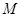 是水平放置的半径足够大的圆盘,绕过其圆心的竖直轴
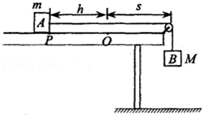
是水平放置的半径足够大的圆盘,绕过其圆心的竖直轴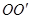 匀速转动,规定经过圆心O水平向右为x轴的正方向.在圆心O正上方距盘面高为h处有一个正在间断滴水的容器,从t=0时刻开始随传送带沿与x轴平行的方向做匀速直线运动,速度大小为
匀速转动,规定经过圆心O水平向右为x轴的正方向.在圆心O正上方距盘面高为h处有一个正在间断滴水的容器,从t=0时刻开始随传送带沿与x轴平行的方向做匀速直线运动,速度大小为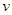 .已知容器在t=0时刻滴下第一滴水,以后每当前一滴水刚好落到盘面上时再滴一滴水.求:
.已知容器在t=0时刻滴下第一滴水,以后每当前一滴水刚好落到盘面上时再滴一滴水.求: