题目内容
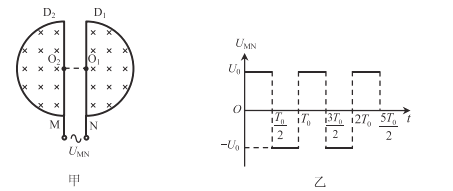
【题目】如图甲，两个半径足够大的D形金属盒D1、D2正对放置，O1、O2分别为两盒的圆心，盒内区域存在与盒面垂直的匀强磁场。加在两盒之间的电压变化规律如图乙，正反向电压的大小均为Uo，周期为To，两盒之间的电场可视为匀强电场。在t=0时刻，将一个质量为m、电荷量为q（q>0）的粒子由O2处静止释放，粒子在电场力的作用下向右运动，在
时刻通过O1.粒子穿过两D形盒边界M、N时运动不受影响，不考虑由于电场变化而产生的磁场的影响，不计粒子重力。
(1)求两D形盒边界M、N之间的距离；
(2)若D1盒内磁场的磁感应强度
，且粒子在D1、D2盒内各运动一次后能到达 O1，求D2盒内磁场的磁感应强度；
(3)若D2、D2盒内磁场的磁感应强度相同，且粒子在D1、D2盒内各运动一次后在t= 2To时刻到达Ol，求磁场的磁感应强度。
【答案】(1) 
(2) 
(3) 
【解析】
(1)设两盒之间的距离为d，盒间电场强度为E，粒子在电场中的加速度为a，则有
U0=Ed
qE=ma
联立解得
(2)设粒子到达O1的速度为v1，在D1盒内运动的半径为R1，周期为T1，时间为t1，则有
可得
t1=T0
故粒子在
时刻回到电场；
设粒子经电场再次加速后以速度v2进入D2盒，由动能定理
设粒子在D2盒内的运动半径为R2，则
粒子在D1D2盒内各运动一次后能到达O2应有
R2=R1
联立各式可得
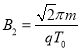
(3)依题意可知粒子在D1D2盒内运动的半径相等；又
故粒子进入D2盒内的速度也为v1；可判断出粒子第二次从O2运动到O1的时间也为
粒子的运动轨迹如图；
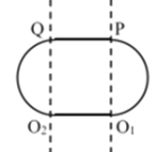
粒子从P到Q先加速后减速，且加速过程的时间和位移均相等，设加速过程的时间为t2，则有
则粒子每次在磁场中运动的时间
又
联立各式解得
天天向上一本好卷系列答案
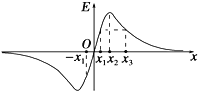
小学生10分钟应用题系列答案
【题目】探究加速度与力、质量的关系，可以采用不同的研究方案。
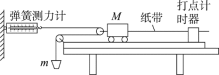
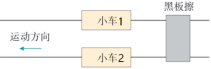
（1）甲同学采用的方案如图所示，将两个相同的小车放在水平木板上，前端各系一条细绳，线的另一端跨过定滑轮各挂一个小盘，盘中可以放不同的砝码，盘与砝码的总重力可以近似认为是小车受到的拉力。两小车后端各系一条细线，用黑板擦可以同时按住或放开这两条细线，使两车同时停止或运动。某次操作中，在相同时间内测得小车的位移分别为x1、x2，若小车的加速度分别为a1、a2，则 a1∶a2=_________，这么做的依据是________________________________。
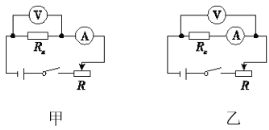
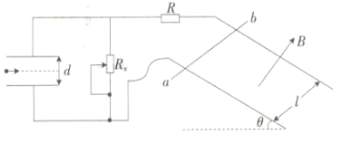
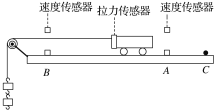
（2）乙同学用如图所示器材进行定量探究。用拉力传感器(能测量拉力的仪器)和速度传感器(能测量瞬时速度的仪器)探究加速度与物体受力的关系。用拉力传感器记录小车受到拉力的大小，在长木板上相距L＝48.0cm的A、B两点各安装一个速度传感器，分别测量小车到达A、B时的速率。
①乙同学认为，运动时小车受到的拉力_____悬挂物的总重力（选填“>”或“<”），所以乙同学采用力传感器进行实验。
②实验主要步骤如下：
Ⅰ、将拉力传感器固定在小车上；
Ⅱ、垫高木板右端，让小车在不受拉力时做__________运动；
Ⅲ、把细线的一端固定在拉力传感器上，另一端通过定滑轮与钩码相连；为保证细线的拉力不变，必须调节滑轮的高度使___________________________________；
Ⅳ、接通电源后自C点释放小车，小车在细线拉动下运动，记录细线拉力F的大小及小车分别到达A、B时的速率vA、vB；
Ⅴ、改变所挂钩码的数量，重复步骤④的操作。
③下表中记录了实验测得的几组数据,
是两个速度传感器记录速度的平方差，则加速度的表达式a＝________（用已知符号表示），请将表中第4次的实验数据填写完整(结果保留三位有效数字)。
次数 | F/N | v－v/(m2·s－2) | a/(m·s－2) |
1 | 0.60 | 0.77 | 0.80 |
2 | 1.04 | 1.61 | 1.68 |
3 | 1.42 | 2.34 | 2.44 |
4 | 2.62 | 4.65 | ________ |
5 | 3.00 | 5.49 | 5.72 |
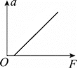
④由表中数据，在坐标纸上作出a－F关系图线______。
⑤对比实验结果与理论计算得到的关系图线(图中已画出理论图线)，造成上述偏差的原因除了拉力传感器读数可能偏大外，还可能是_____________________。
