题目内容
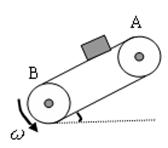
 如图所示,传送带与地面倾角θ=37°,A→B长度为L=16m,传送带以v0=10m/s的速率逆时针转动,在传送带上端A无初速度地释放一个质量为0.5kg的物体,它与传送带之间的动摩擦因数为0.5.求:
如图所示,传送带与地面倾角θ=37°,A→B长度为L=16m,传送带以v0=10m/s的速率逆时针转动,在传送带上端A无初速度地释放一个质量为0.5kg的物体,它与传送带之间的动摩擦因数为0.5.求:(1)物体在A处时的加速度;
(2)物体在B处时的加速度;
(3)物体从A运动到B需时间是多少?
分析:(1)物体放在传送带上后,开始阶段,传送带的速度大于物体的速度,传送带给物体一沿斜面向下的滑动摩擦力,物体由静止开始加速下滑,当物体加速至与传送带速度相等时,由于μ<tanθ,物体在重力作用下将继续加速,此后物体的速度大于传送带的速度,传送带给物体沿传送带向上的滑动摩擦力,但合力沿传送带向下,物体继续加速下滑,综上可知,滑动摩擦力的方向在获得共同速度的瞬间发生了“突变”.
解答:解:(1)开始阶段由牛顿第二定律得:mgsinθ+μmgcosθ=ma1 所以:a1=gsinθ+μgcosθ=10m/s2
(2)物体加速至与传送带速度相等时需要的时间t1=
=1s;
发生的位移:s=
a1 t12=5m<16m,所以物体加速到10m/s 时仍未到达B点,此时摩擦力方向改变.
第二阶段有:mgsinθ-μmgcosθ=ma2;所以:a2=2m/s2
所以物体在B处时的加速度为2m/s2
(3)设第二阶段物体滑动到B 的时间为t2则:
LAB-S=vt2+
a2t22
解得:t2=1s
故物体经历的总时间t=t1+t2=2s.
答:(1)物体在A处时的加速度为10m/s2;(2)物体在B处时的加速度为2m/s2;(3)物体从A运动到B需时间是2s.
(2)物体加速至与传送带速度相等时需要的时间t1=
| v |
| a1 |
发生的位移:s=
| 1 |
| 2 |
第二阶段有:mgsinθ-μmgcosθ=ma2;所以:a2=2m/s2
所以物体在B处时的加速度为2m/s2
(3)设第二阶段物体滑动到B 的时间为t2则:
LAB-S=vt2+
| 1 |
| 2 |
解得:t2=1s
故物体经历的总时间t=t1+t2=2s.
答:(1)物体在A处时的加速度为10m/s2;(2)物体在B处时的加速度为2m/s2;(3)物体从A运动到B需时间是2s.
点评:从上述例题可以总结出,皮带传送物体所受摩擦力可能发生突变,不论是其大小的突变,还是其方向的突变,都发生在物体的速度与传送带速度相等的时刻.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
 如图所示,传送带与地面的倾角θ,传送带以v匀速运动,在传送带底端无初速地放置一个质量为m的物体,当物体上升高度h时,物体已经相对传动带静止,在这个过程中分析正确的是( )
如图所示,传送带与地面的倾角θ,传送带以v匀速运动,在传送带底端无初速地放置一个质量为m的物体,当物体上升高度h时,物体已经相对传动带静止,在这个过程中分析正确的是( ) 如图所示,传送带与地面的倾角θ=37°,从A端到B端的长度为29m,传送带以v0=10m/s的速度沿逆时针方向转动.在传送带上端A处无初速地放置一个质量为0.5kg的物体,它与传送带之间的动摩擦因数为μ=0.5,求物体从A端运动到B端所需的时间是多少?(sin37°=0.6,cos37°=0.8)
如图所示,传送带与地面的倾角θ=37°,从A端到B端的长度为29m,传送带以v0=10m/s的速度沿逆时针方向转动.在传送带上端A处无初速地放置一个质量为0.5kg的物体,它与传送带之间的动摩擦因数为μ=0.5,求物体从A端运动到B端所需的时间是多少?(sin37°=0.6,cos37°=0.8)