题目内容
【题目】卫星发射进入预定轨道往往需要进行多次轨道调整，如图所示，某次发射任务中先将卫星送至 近地轨道，然后再控制卫星进入椭圆轨道，最后进入预定圆形轨道运动。图中 O 点为地心，A 点 是近地轨道和椭圆轨道的交点，B 点是远地轨道与椭圆轨道的交点，远地点 B离地面高度为 6R（R 为地球半径）。设卫星在近地轨道运动的周期为 T，下列 说法正确的是 （ ）
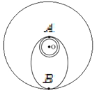
A. 控制卫星从图中低轨道进入椭圆轨道需要使卫星减速
B. 卫星在近地轨道与远地轨道运动的速度之比为
:1
C. 卫星从 A 点经 4 T 的时间刚好能到达 B 点
D. 卫星在近地轨道通过 A 点的加速度小于在椭圆轨道通过 A 点时的加速度
【答案】C
【解析】
控制卫星从图中低轨道进入椭圆轨道时需做离心运动，可知需要的向心力增大，所以需要加速才能实现。故A错误。近地圆轨道1与远地圆轨道的半径分别为R和7R，根据卫星的线速度公式
知，卫星在近地圆轨道1与远地圆轨道运动2的速度之比
：1，故B错误。卫星在椭圆轨道上的半长轴：a=
=4R．由开普勒第三定律
=K，可得：
，有 T椭圆=8T；卫星在椭圆轨道上运动时，由近地点A到远地点B的过程恰好等于椭圆的运动的半个周期，所以：
．故C正确。根据牛顿第二定律和万有引力定律得：G
=ma，得 a=
，所以卫星在近地轨道通过A点的加速度等于卫星在椭圆轨道上通过A点的加速度。故D错误。故选C。
练习册系列答案
相关题目
