题目内容
(10分)如图所示,足够长的斜面AB的倾角为β,斜面下端与光滑的圆弧轨道BCDE的B端相切,C为圆弧的最低点,圆弧半径为R。现有一质量为m的小物体从斜面上的某处无初速度的滑下,已知物体与斜面间的动摩擦因素为μ。
求:(1)要使小球通过圆弧轨道的最高点,则释放点距斜面的底端至少多高?
(2)若在斜面上与D点等高处释放,小物体在运动过程中通过C点时,对轨道的最小压力?
(1)h= 
(2)3 mg-2mgcosβ,方向竖直向下
解析:(1)要使小球恰好通过圆弧轨道的最高点,则要求小球通过最高点时的速度应满足: ![]() ……………①
……………①
由释放点到该点由动能定理有
mg(h-R-Rcosβ)- μmgcosβh/sinβ=![]() ……………②
……………②
得h= ![]() ……………③
……………③
(2)从与D点等高处释放后,由于斜面摩擦的原因,小球最终将在圆弧上做往复运动,其左侧最高点为B点,由机械能守恒得:
mg(R-Rcosβ)=![]() ……………④
……………④
由向心力公式得:N-mg=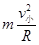 ……………⑤
……………⑤
得 N= 3mg-2mgcosβ ……………⑥
由牛顿第三定律得:
小球对轨道的最小压力大小为3 mg-2mgco sβ,方向竖直向下……………⑦
评分标准:①②⑤各2分;③④⑥⑦各1分

练习册系列答案
相关题目
 (2013?绵阳模拟)如图所示,足够长的斜面上有a、b、c、d、e五个点,ab=bc=cd=de,从a点水平抛出一 个小球,初速度为v时,小球落在斜面上的b点,落在斜面上时的速度方向与斜面夹角为θ;不计空气阻力,初速度为2v时( )
(2013?绵阳模拟)如图所示,足够长的斜面上有a、b、c、d、e五个点,ab=bc=cd=de,从a点水平抛出一 个小球,初速度为v时,小球落在斜面上的b点,落在斜面上时的速度方向与斜面夹角为θ;不计空气阻力,初速度为2v时( )

