题目内容
【题目】如图所示,平行导轨倾斜放置,倾角θ=37°,匀强磁场的方向垂直于导轨平面向上,磁感应强度B=![]() T,质量为m=1kg的金属棒ab垂直放在导轨上,ab与导轨平面间的动摩擦因数μ=0.25。ab的电阻r=1Ω,平行导轨间的距离L=1m, R1 =R2=4Ω,导轨电阻不计,ab由静止开始下滑运动x=3.5m后达到匀速。sin37°=0.6,cos37°=0.8.求:
T,质量为m=1kg的金属棒ab垂直放在导轨上,ab与导轨平面间的动摩擦因数μ=0.25。ab的电阻r=1Ω,平行导轨间的距离L=1m, R1 =R2=4Ω,导轨电阻不计,ab由静止开始下滑运动x=3.5m后达到匀速。sin37°=0.6,cos37°=0.8.求:
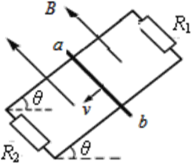
(1)ab在导轨上匀速下滑的速度多大?
(2)ab由静止到匀速过程中电路产生的焦耳热为多少?
【答案】(1)4m/s(2)6J
【解析】
(1)ab在导轨上匀速下滑时ab棒受力平衡,推导出安培力与速度的关系,由平衡条件即可求得速度.
(2)根据能量守恒定律或动能定理求解焦耳热.
(1)ab由静止开始下滑,速度不断增大,对ab受力分析如图所示: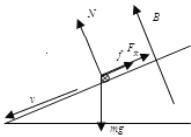
由牛顿第二定律mgsinθ-μmgcosθ-BIL=ma
可知,ab做加速度减小的加速运动,当加速度减小到零时,速度增加到最大,此后以最大速度做匀速运动.
故ab在导轨上匀速下滑时mgsinθ-μmgcosθ-BIL=0 ①
等效电路如图所示,:
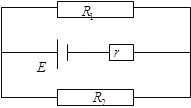
外电路电阻![]() =4Ω ②
=4Ω ②
电路中总电阻R总=r+R=5Ω ③
由闭合电路的欧姆定律和法拉第电磁感应定律可知:
电路中的电流![]() ④
④
此时的感应电动势E=BLv ⑤
由①③④⑤解得:ab在导轨上匀速下滑的速度v=4m/s ⑥
(2)由于ab下滑过程速度不断变化,感应电动势和电流不恒定,故不能用焦耳定律求焦耳热.
根据能量守恒定律,ab减少的重力势能等于ab增加的动能、克服摩擦力做功产生的内能与电路中总的焦耳热之和,即![]() ⑩
⑩
展开得![]()
解得电路中总的焦耳热:Q=6J

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目