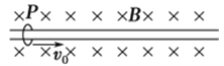题目内容
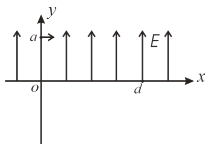
【题目】如图所示,在xoy坐标系中,y>0的范围内存在着沿y轴正方向的匀强电场,在y<0的范围内存在着垂直纸面的匀强磁场(方向未画出)。现有一质量为m,电荷量大小为-q(重力不计)的带电粒子,以初速度v0(v0沿x轴正方向)从y轴上的a点出发,运动一段时间后,恰好从x轴上的d点第一次进入磁场,然后从O点第—次离开磁场。已知oa=L,od=2L,求
（1）电场强度;
（2）磁感应强度的大小和方向。
【答案】(1)
(2)
【解析】
运用运动的合成与分解，结合牛顿第二定律与运动学规律结合即可求出E的大小；洛伦兹力提供向心力结合圆周运动的规律，再与几何关系结合可求磁感应强度的大小；根据左手定则确定磁感应强度的方向；
解：(1)粒子在匀强电场中做类平抛运动
x方向：
①
y方向：
②
根据牛顿第二定律得：
③
由①②③式得：电场强度
(2)设粒子在电场中出射时，沿y方向的速度大小为vy，速度方向与x轴正方向的夹角为α，
y方向：
④
联立①②④式得：
,所以
所以粒子进入磁场时速度大小：
⑤
画出粒子的运动轨迹如图，根据左手定则可知磁场方向垂直纸面向里
根据洛伦兹力提供向心力有：
⑥
根据几何关系有：
⑦
由⑤⑥⑦式得：
练习册系列答案
开心蛙口算题卡系列答案
相关题目
