Question

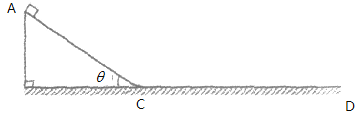
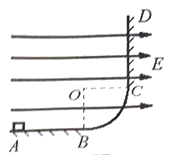
【题目】在竖直平面内，AB为水平放置的绝缘粗糙轨道，CD为竖直放置的足够长绝缘粗糙轨道，AB与CD通过四分之一绝缘光滑圆弧形轨道平滑连接，圆弧的圆心为O，半径R=1.0m，轨道所在空间存在水平向右的匀强电场，电场强度的大小，现有质量m=0.20kg，电荷量的带电体(可视为质点)，从A点由静止开始向右运动，已知A、B间距离L=1.0m，带电体与轨道AB、CD的动摩擦因数均为=0.5。假定带电体与轨道之间的最大静摩擦力等于滑动摩擦力，不计空气阻力。求：

（1）带电体运动到圆弧形轨道C点时对轨道的压力大小；

（2）带电体最终停止的位置；

（3）从A点到停止运动过程中带电体的电势能变化量；

（4）为使带电体从最终停止处又能回到A点，可在该处给带电体一个水平的速度， 求这速度大小和方向。

Answer 1

【答案】（1）24N；（2）带电体最终静止在C点正上方与C的竖直距离为1.8m处；（3）电势能的变化量Ep=-12J；（4）速度大小为m/s，方向水平向左。

【解析】

（1）设带电体达到C时速度为v，由动能定理

qE(L+R)-mgL-mgR=mv2-0

解得v=m/s，在C点，根据牛顿第二定律

FN-qE=m

解得带电体运动到圆弧形轨道C点时轨道对它的支持力FN=24N，根据牛顿第三定律知，带电体运动到圆弧形轨道C点时对轨道的压力大小也是24N。

（2）设带电体沿竖直轨道CD上升的最大高度为h，由动能定理

-mgh-qEh=0-mv2

解得h=1.8m，在最高点带电体受到的最大静摩擦力Fmax=qE=3N，重力G=mg=2N，所以带电体最终静止在C点正上方与C的竖直距离为1.8m处。

（3）从A点到停止运动过程中电场力做的功

W=qE(L+R)=12J

从A点到停止运动过程中带电体的电势能变化量

Ep=-W=-12J

（4）为使带电体从最终停止处又能回到A点，设在停止处给带电体一个方向向左的初速度v0，带电体水平方向做匀减速运动，竖直方向做匀加速运动，要能回到A点，水平方向的加速度a==30m/s2，水平方向的位移

L+R=v0t-at2

竖直方向的位移

h+R=gt2

解得v0=m/s，方向水平向左。

答：（1）带电体运动到圆弧形轨道C点时对轨道的压力大小是24N；（2）带电体最终静止在C点正上方与C的竖直距离为1.8m处；（3）电势能变化量为-12J；（4）水平的速度的大小为m/s，方向水平向左。