题目内容
7.一列火车起动后做匀加速直线运动,从站台驶出,一人站在第1节车厢前端进行观测,第1节车厢经过他身旁的时间为6s,全部车厢经过他身旁共历时24s,每节车厢长度相等且连续处长度不计,求:(1)这列火车共有多少节车厢.
(2)这过程中最后六秒内有多少节车厢通过他身旁.
(3)最后一节车厢通过他身旁的时间.
(4)第五节至第十六节车厢通过他的时间.
分析 (1)根据匀变速直线运动的位移时间公式,通过类比得出这列火车车厢的节数.
(2)根据位移时间公式得出最后6s内的位移,从而得出车厢的节数.
(3)根据初速度为零的匀加速直线运动的推论,结合第一节车厢通过他身旁的时间,求出最后一节车厢通过他身旁的时间.
(4)根据位移时间公式求出前五节车厢和前十六节车厢通过他的时间,从而得出第五节至第十六节车厢通过他的时间.
解答 解:(1)第1节车厢经过他身旁的时间为6s,根据位移时间公式有:$L=\frac{1}{2}a{{t}_{1}}^{2}$,
全部车厢经过他身旁共历时24s,根据位移时间公式有:$s=\frac{1}{2}a{{t}_{2}}^{2}$,
因为t2=4t1,则s=16L,可知这列火车共有16节车厢.
(2)最后6s内通过的位移$x=s-\frac{1}{2}a{{t}_{3}}^{2}$,因为t3=24-6s=18s,
则$\frac{1}{2}a{{t}_{3}}^{2}$=9L,所以x=7L,
可知最后6s内有7节车厢通过他身旁.
(3)初速度为零的匀加速直线运动,在通过连续相等位移内所用的时间之比为1:($\sqrt{2}-1$):($\sqrt{3}-\sqrt{2}$):…($\sqrt{n}-\sqrt{n-1}$),
则第一节车厢和最后一节车厢通过他的时间之比为$1:(4-\sqrt{15})$,
第1节车厢经过他身旁的时间为6s,则最后一节车厢通过他的时间为$(24-4\sqrt{15})$s.
(4)前五节车厢,有:5L=$\frac{1}{2}at{′}^{2}$,
前16节车厢,有:16L=$\frac{1}{2}at{′′}^{2}$,
又$L=\frac{1}{2}a{{t}_{1}}^{2}$,
解得$t′=\sqrt{5}{t}_{1}=6\sqrt{5}s$,t″=4t1=24s,
则第五节至第十六节车厢通过他的时间△t=t″-t′=(24-$6\sqrt{5}$)s.
答:(1)这列火车共有16节车厢.
(2)这过程中最后六秒内有7节车厢通过他身旁.
(3)最后一节车厢通过他身旁的时间为$(24-4\sqrt{15})$s.
(4)第五节至第十六节车厢通过他的时间为(24-$6\sqrt{5}$)s.
点评 解决本题的关键掌握匀变速直线运动的运动学公式和推论,并能灵活运用,有时运用推论求解会使问题更加简捷.

 如图所示的平行板器件中电场强度E与磁感应强度B垂直,这种装置能把具有某一特定速度的粒子选择出来,所以叫做速度选择器.若一带正电(+q)的粒子以速度v从左边小孔射入恰沿着图中虚线路径通过这个速度选择器,则( )
如图所示的平行板器件中电场强度E与磁感应强度B垂直,这种装置能把具有某一特定速度的粒子选择出来,所以叫做速度选择器.若一带正电(+q)的粒子以速度v从左边小孔射入恰沿着图中虚线路径通过这个速度选择器,则( )| A. | 若该粒子以速度v从右边射入仍能沿着图中虚线路径通过这个速度选择器 | |
| B. | 若一带负电(-q)的粒子以速度v从右边射入也恰沿着图中虚线路径通过这个速度选择器 | |
| C. | 若一带负电(-q)的粒子以速度v从左边射入也恰沿着图中虚线路径通过这个速度选择器 | |
| D. | 若一带负电(-q)的粒子以速度v从左边射入将向上极板偏转 |
| A. | 伽利略通过“理想实验”得出结论:一旦物体具有某一速度,如果它不受力,它将以这一速度永远运动下去 | |
| B. | 牛顿认为,物体具有保持原来匀速直线运动状态或静止状态的性质 | |
| C. | 牛顿第一定律、牛顿第二定律都可以通过实验来验证 | |
| D. | 国际单位制中,kg、m、N是三个基本单位 | |
| E. | 根据速度定义式v=$\frac{△x}{△t}$,当△t→0时,$\frac{△x}{△t}$就可以表示物体在t时刻的瞬时速度,该定义运用了极限思维法 |
(1)若只有这6个计数点,有那些计数点的瞬时速度不可测量A、F,根据所学知识可以求出AC的平均速度是0.355m/s.
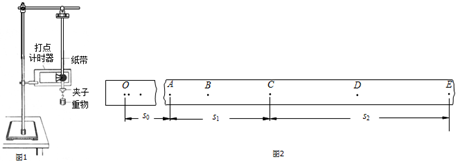
(2)由纸带提供的数据求出打下点B、D瞬时速度
| 计数点序号 | B | C | D | E |
| 对应时刻t/s | 0.1 | 0.2 | 0.3 | 0.4 |
| 小车的速度v/(m•s-1) | 0.355 | 0.400 | 0.455 | 0.500 |
(4)根据作出的v-t图线可得小车运动的加速度为0.50 m/s2.(保留两位有效数字)

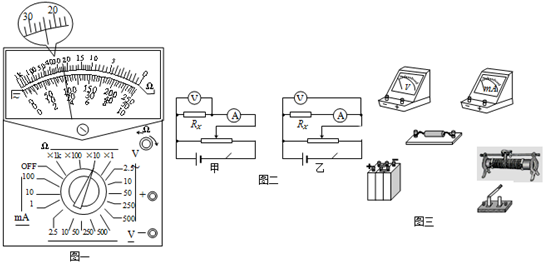
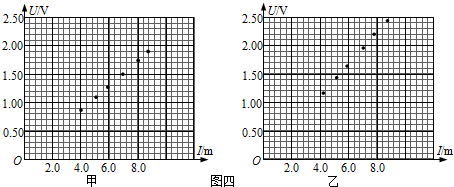
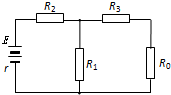 如图所示电路中,R2=R3=R为了使R0上的电压为把它直接与电源相接时的电压的$\frac{1}{k}$,并且电池消耗的功率相同,那么应如何选择R1和R0.
如图所示电路中,R2=R3=R为了使R0上的电压为把它直接与电源相接时的电压的$\frac{1}{k}$,并且电池消耗的功率相同,那么应如何选择R1和R0.