题目内容
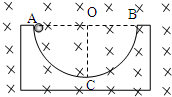 如图所示,半径为R的半圆形槽放在粗糙的水平地面上,槽内部光滑,其质量为M.匀强磁场与槽面垂直向内,将质量为m的带电小球自槽口A处由静止释放,小球到达槽最低点C时,恰好对槽无压力.整个过程中M对地始终静止,问:
如图所示,半径为R的半圆形槽放在粗糙的水平地面上,槽内部光滑,其质量为M.匀强磁场与槽面垂直向内,将质量为m的带电小球自槽口A处由静止释放,小球到达槽最低点C时,恰好对槽无压力.整个过程中M对地始终静止,问:(1)小球第一次运动到C点时,速度大小为多少?
(2)小球在以后运动过程中,半圆形槽对地面的最大压力是多少?
分析:(1)从A到C,支持力和洛伦兹力不做功,只有重力做功,根据动能定理求出第一次运动到C点时的速度.
(2)小球由右向左运动到槽最低点时,重力向下,洛伦兹力向下,支持力向上,合力提供向心力,此时小球对槽压力最大,此时有F-mg-qvB=m
.根据A处由静止释放,小球到达槽最低点C时,恰好对槽无压力有qvB-mg=m
,联立两式得出小球对槽的最大压力,再对半圆形槽受力分析,得出半圆槽对地面的最大压力.
(2)小球由右向左运动到槽最低点时,重力向下,洛伦兹力向下,支持力向上,合力提供向心力,此时小球对槽压力最大,此时有F-mg-qvB=m
| v2 |
| R |
| v2 |
| R |
解答:解:(1)从A至C
mgR=
mv2
v=
故第一次运动到C点时的速度为
.
(2)小球由右向左运动到槽最低点时,小球对槽压力最大,槽对地压力最大
对球 F-mg-qvB=m
又小球由左向右运动到最低点时,对小球
qvB-mg=m
则 F=2(mg+m
)=6mg
当小球运动到最低点时,槽对地压力FM=6mg+Mg
故槽对地面的最大压力为FM=6mg+Mg.
mgR=
| 1 |
| 2 |
v=
| 2gR |
故第一次运动到C点时的速度为
| 2gR |
(2)小球由右向左运动到槽最低点时,小球对槽压力最大,槽对地压力最大
对球 F-mg-qvB=m
| v2 |
| R |
又小球由左向右运动到最低点时,对小球
qvB-mg=m
| v2 |
| R |
则 F=2(mg+m
| v2 |
| R |
当小球运动到最低点时,槽对地压力FM=6mg+Mg
故槽对地面的最大压力为FM=6mg+Mg.
点评:解决本题的关键知道洛伦兹力不做功,只有重力做功,所以小球向左向右通过最低点的速度大小不变.知道小球从右向左运动到槽最低点时,小球对槽压力最大,槽对地压力最大.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
 如图所示,半径为R的光滑半圆轨道竖直放置,两个质量均为m的小球A、B以不同的速率进入轨道,A通过最高点C时,对轨道的压力为3mg,B通过最高点C时,对轨道的压力恰好为零,求:
如图所示,半径为R的光滑半圆轨道竖直放置,两个质量均为m的小球A、B以不同的速率进入轨道,A通过最高点C时,对轨道的压力为3mg,B通过最高点C时,对轨道的压力恰好为零,求: 如图所示,半径为R的vt-sB=l光滑圆弧轨道竖直放置,底端与光滑的水平轨道相接,质量为m的小球B静止光滑水平轨道上,其左侧连接了一轻质弹簧,质量为m的小球A自圆弧轨道的顶端由静止释放,重力加速度为g,小球可视为质点.
如图所示,半径为R的vt-sB=l光滑圆弧轨道竖直放置,底端与光滑的水平轨道相接,质量为m的小球B静止光滑水平轨道上,其左侧连接了一轻质弹簧,质量为m的小球A自圆弧轨道的顶端由静止释放,重力加速度为g,小球可视为质点. 如图所示,半径为R的
如图所示,半径为R的 如图所示,半径为R的半圆轨道BC竖直放置.一个质量为m 的小球以某一初速度从A点出发,经AB段进入半圆轨道,在B点时对轨道的压力为7mg,之后向上运动完成半个圆周运动恰好到达C点.试求:
如图所示,半径为R的半圆轨道BC竖直放置.一个质量为m 的小球以某一初速度从A点出发,经AB段进入半圆轨道,在B点时对轨道的压力为7mg,之后向上运动完成半个圆周运动恰好到达C点.试求: 如图所示,半径为r的圆筒,绕竖直中心轴OO′旋转,小物块a靠在圆筒的内壁上,它与圆筒内壁间的动摩擦因数为μ,现要使a不下落,则圆筒转动的角速度ω至少为( )
如图所示,半径为r的圆筒,绕竖直中心轴OO′旋转,小物块a靠在圆筒的内壁上,它与圆筒内壁间的动摩擦因数为μ,现要使a不下落,则圆筒转动的角速度ω至少为( )