题目内容
【题目】如图所示,光滑绝缘轨道由水平段AB和圆形轨道BCD组成,B在圆心正下方,轨道上的C、D两点与圆心等高,圆轨道半径为R。整个装置处在水平向右的匀强电场中,电场强度大小为E=![]() 。现将一小球从A点由静止释放。已知小球质量为m,电量为q,且带正电,重力加速度为g,不计空气阻力,求:
。现将一小球从A点由静止释放。已知小球质量为m,电量为q,且带正电,重力加速度为g,不计空气阻力,求:
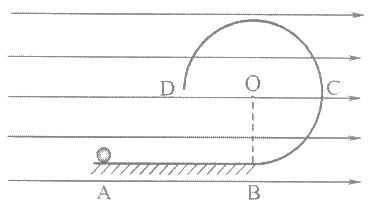
(1)若AB=2R,求小球运动到C点时对轨道的压力大小;
(2)若小球能沿圆轨道运动到D点,则AB间的距离至少为多大?
【答案】(1)N=5mg;(2)![]()
【解析】
(1)小球从A点到C点由动能定理有:
![]()
在C点由牛顿第二定律得:
![]()
联立解得:![]()
由牛顿第三定律可知,球运动到C点时对轨道的压力大小为5mg;
(2)电场与重力场的合场强与竖直方向成![]() 斜向下,设AB的距离为x,
斜向下,设AB的距离为x,
球能沿圆轨道运动到D点,则在D点有:
![]()
从A到D由动能定理得:
![]()
联立解得:![]()

 阅读快车系列答案
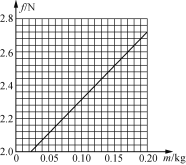
阅读快车系列答案【题目】目前很多用电器的指示灯是发光二极管.某厂家提供的某种型号发光二极管的伏安特性曲线如图所示,该二极管的正常工作电压为3.0V,允许通过的最大电流为56mA.

(1)该二极管正常工作时阻值为________Ω.
(2)某同学先用中值电阻为15Ω的多用电表欧姆挡测量该二极管的正向电阻,下列测量方法正确的是________.

(3)利用下列实验器材,验证该元件的伏安特性曲线与厂家提供的是否一致.
实验器材名称 | 规格 |
待测的发光二极管 | |
直流电源E | 电动势4.5V,内阻忽略不计 |
滑动变阻器R | 最大阻值为20Ω |
电压表V1 | 量程10V,内阻约50kΩ |
电压表V2 | 量程5V,内阻约20kΩ |
电流表A1 | 量程100mA,内阻约50Ω |
电流表A2 | 量程60mA,内阻约100Ω |
电键S | |
导线若干 |
①为准确、方便地进行测量,电压表应选用________,电流表应选用________.(填字母符号)
②利用现有器材设计实验电路图,并在虚线框内画出______.