Question

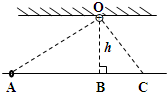（2013?浦东新区一模）如图所示，水平放置的光滑绝缘杆上B点的正上方O点固定一个带电量为Q=+6.0×10^-8C的点电荷，BO相距h=0.24m，B点左侧的A点处套有一个带电量为q=-5.0×10^-9C、质量为m=2.0×10^-4kg带电小圆环，已知∠OAB=37°．C为杆上B点右侧的另一点，∠OCB=53°．
已知由点电荷+Q产生的电场中，距离该点电荷为r处的电势为φ=k

Q

r

，其中k为静电力恒量，k=9.0×10⁹ N?m²/C²．（sin37°=0.6，sin53°=0.8）．试问：
（1）点电荷Q在A、B、C三点产生的电势φ_A、φ_B、φ_C分别多大？
（2）将带电小圆环从A点由静止释放，它到达C点时速度多大？
（3）若将圆环带电量改为qˊ=+1.0×10^-8C，并给其一个指向C点的初速度，则初速度v₀至少多大才能使其到达C点？

Answer 1

分析：（1）由数学知识得到A、B、C三点到Q点电荷的距离r，由φ=k

Q

r

求出三点的电势．
（2）带电小圆环从A点到C点的过程中，电场力做功qU_AC=q（φ_A-φ_C），其他力不做功，根据动能定理求解到达C点时速度．
（3）圆环改为带正电后，沿杆向右运动时先要克服电场力做功到达B点，然后电场力做正功使其到达C点，圆环至少要能到达B点，即到达B点时速度应等于零，根据动能定理研究圆环从A到B的过程，求解初速度．

解答：解：（1）根据题给公式φ=k

Q

r

，有
φA=k

Q

h sin37°

=k

Qsin37°

h

=9.0×109×

6.0×10-8×0.6

0.24

V=1350V
φB=k

Q

h

=9.0×109×

6.0×10-8

0.24

V=2250V
φC=k

Q

h sin53°

=k

Qsin53°

h

=9.0×109×

6.0×10-8×0.8

0.24

V=1800V
（2）设圆环到达C点时速度为v_C，根据动能定理，有
  qUAC=

1

2

mvC2
即q(φA-φC)=

1

2

mvC2
得vC=

2q(φA-φC) m

=

2×(-5.0×10-9)(1350-1800) 2.0×10-4

m/s=0.15m/s
（3）圆环改为带正电后，沿杆向右运动时先要克服电场力做功到达B点，然后电场力做正功使其到达C点，所以对圆环初速度v₀的要求是至少要能到达B点，即到达B点时速度应等于零．
根据动能定理，有q′UAB=0-

1

2

mv02
即q′(φB-φA)=

1

2

mv02
vB=

2q′(φB-φA) m

=

2×1.0×10-8×(2250-1350) 2.0×10-4

m/s=0.30m/s
所以初速度v₀至少为0.30m/s才能使其到达C点．
答：
（1）点电荷Q在A、B、C三点产生的电势φ_A、φ_B、φ_C分别是1350V，2250V和1800V．
（2）将带电小圆环从A点由静止释放，它到达C点时速度是0.15m/s．
（3）若将圆环带电量改为qˊ=+1.0×10^-8C，初速度v₀至少为0.30m/s才能使其到达C点．

点评：本题是信息题，要抓住题给的公式φ=k

Q

r

求解电势，可确定电势差，求出电场力做功．第3问，要注意分析临界条件．