题目内容
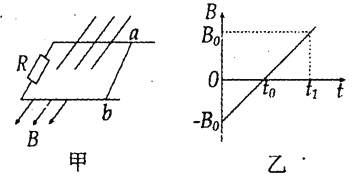
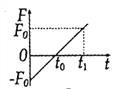
【题目】如图甲所示,一质量为M的长木板静置于光滑水平面上,其上放置一质量为m小滑块.木板受到随时间t变化的水平拉力F作用时,用传感器测出长木板的加速度a与水平拉力F的关系如图乙所示,取g=10m/s2,则( )
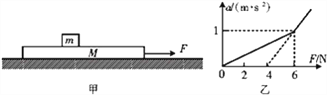
A. 滑块的质量m=2kg,木板的质量M=4kg
B. 当F=8N时,滑块的加速度为1m/s2
C. 滑块与木板之间的滑动摩擦因数为0.2
D. 当0<F<6N时,滑块与木板之间的摩擦力随F变化的函数关系f=2/3F
【答案】BD
【解析】当F等于6N时,加速度为:a=1m/s2,对整体分析,由牛顿第二定律有:F=(M+m)a,代入数据解得:M+m=6kg,当F大于6N时,根据牛顿第二定律得![]() ,图象斜率
,图象斜率![]() ,解得:M=2kg,滑块的质量m=4kg,选项A错误;根据F大于6N的图线知,F=4时,a=0,即:
,解得:M=2kg,滑块的质量m=4kg,选项A错误;根据F大于6N的图线知,F=4时,a=0,即: ![]() ,解得:μ=0.1,a=
,解得:μ=0.1,a=![]() F-2,当F=8N时,长木板的加速度为:a=2m/s2;根据μmg=ma′得:滑块的加速度为 a′=μg=1m/s2,故B正确,C错误.当0<F<6N时,由牛顿第二定律得,对系统:F=(M+m)a,对m:f=ma,解得:f=
F-2,当F=8N时,长木板的加速度为:a=2m/s2;根据μmg=ma′得:滑块的加速度为 a′=μg=1m/s2,故B正确,C错误.当0<F<6N时,由牛顿第二定律得,对系统:F=(M+m)a,对m:f=ma,解得:f=![]() F,故D正确;故选BD.
F,故D正确;故选BD.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目