题目内容
1.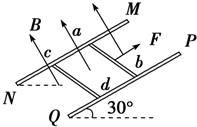 如图所示,两根足够长的光滑平行金属导轨MN、PQ间距为L=0.5m,其电阻不计,两导轨及其构成的平面与水平面成30°角.完全相同的两金属棒ab、cd分别垂直导轨放置,每棒两端都与导轨始终良好接触,已知两棒质量均为m=0.02kg,电阻均为R=0.1Ω,整个装置处在垂直于导轨平面向上的匀强磁场中,磁感应强度B=0.2T,棒ab在平行于导轨向上的力F作用下,沿导轨向上匀速运动,而棒cd恰好能够保持静止.g取10m/s2,
如图所示,两根足够长的光滑平行金属导轨MN、PQ间距为L=0.5m,其电阻不计,两导轨及其构成的平面与水平面成30°角.完全相同的两金属棒ab、cd分别垂直导轨放置,每棒两端都与导轨始终良好接触,已知两棒质量均为m=0.02kg,电阻均为R=0.1Ω,整个装置处在垂直于导轨平面向上的匀强磁场中,磁感应强度B=0.2T,棒ab在平行于导轨向上的力F作用下,沿导轨向上匀速运动,而棒cd恰好能够保持静止.g取10m/s2,问:(1)通过棒cd的电流I是多少,方向如何?
(2)棒ab受到的力F多大?
(3)棒cd每产生Q=0.1J的热量,力F做的功W是多少?
分析 (1)对cd研究:cd保持静止,分析受力情况,由平衡条件求出安培力大小,即能由安培力公式F=BIL求出电流的大小,由左手定则判断I的方向.
(2)再对棒ab研究,棒ab沿导轨向上匀速运动,由平衡条件求出F.
(3)两棒电阻相等,产生的热量相等.由功能关系求得力F做的功.
解答 解:(1)棒cd受到的安培力为:Fcd=BIL…①
棒cd在共点力作用下平衡,则有:Fcd=mgsin30°…②
由①②式得:BIL=mgsin30°
解得:I=$\frac{mgsin30°}{BL}$=$\frac{0.02×10×0.5}{0.2×0.5}$A=1A,方向由右手定则可知由d到c.
(2)棒ab与棒cd受到的安培力大小相等Fab=Fcd
对棒ab由共点力平衡有:F=mgsin30°+BIL
代入数据解得:F=2mgsin30°=0.2N
(3)设ab棒匀速运动的速度大小为v,则产生的感应电动势:E=BLv
由闭合电路欧姆定律知:I=$\frac{E}{2R}$
联立得:2IR=Blv,v=$\frac{2IR}{BL}$m/s=2m/s
设在时间t内棒cd产生Q=0.1J热量,由焦耳定律可知:Q=I2Rt
则得:t=$\frac{Q}{{I}^{2}R}$=$\frac{0.1}{{1}^{2}×0.1}$s=1s
在时间t内,棒ab沿导轨的位移:x=vt
力F做的功:W=Fx=Fvt=0.2×2×1J=0.4J
答:(1)通过cd棒的电流I是1A,方向d→c.
(2)棒ab受到的力F是0.2N.
(3)棒力F做的功W是0.4J
点评 本题是电磁感应中的力学问题,综合运用电磁磁学知识和力平衡知识.第2问题,也可以选择研究整体求解F的大小.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
9. 在做“用单摆测定重力加速度”的实验中.
在做“用单摆测定重力加速度”的实验中.
(1)如果测得的g值偏大,可能的原因是D(填写字母代号)
A.测摆长时,忘记了摆球的半径
B.摆线上端悬点未固定牢,摆动中出现松动,使摆线长度增加了
C.开始计时时,秒表过早按下
D.实验中误将49次全振动次数记为50次
(2)某同学在实验中,测量6种不同摆长l情况下单摆的振动周期T,记录实验数据如下:
请以l为横坐标,T2为纵坐标,在如图1中作出T2-l图线,并利用此图线得重力加速度g=9.86m/s2.(取π2=9.86,结果保留三位有效数字)
(3)一位同学查阅资料得知,单摆在最大摆角θ较大时周期公式可近似表述为T=2π(1+$\frac{1}{4}$sin2$\frac{θ}{2}$)$\sqrt{\frac{l}{g}}$.为了用图象法验证单摆周期T和最大摆角θ的关系,他测出摆长为l的同一单摆在不同最大摆角θ时的周期T,并根据实验数据描绘出如图2所示的图线.根据所给周期公式可知,图中的纵轴表示的是sin2$\frac{θ}{2}$,图线延长后与横轴交点的横坐标为$2π\sqrt{\frac{l}{g}}$.
 在做“用单摆测定重力加速度”的实验中.
在做“用单摆测定重力加速度”的实验中.(1)如果测得的g值偏大,可能的原因是D(填写字母代号)
A.测摆长时,忘记了摆球的半径
B.摆线上端悬点未固定牢,摆动中出现松动,使摆线长度增加了
C.开始计时时,秒表过早按下
D.实验中误将49次全振动次数记为50次
(2)某同学在实验中,测量6种不同摆长l情况下单摆的振动周期T,记录实验数据如下:
| l/m | 0.4 | 0.5 | 0.8 | 0.9 | 1.0 | 1.2 |
| T/s | 1.26 | 1.42 | 1.79 | 1.90 | 2.00 | 2.20 |
| T2/s2 | 1.59 | 2.02 | 3.20 | 3.61 | 4.00 | 4.84 |
(3)一位同学查阅资料得知,单摆在最大摆角θ较大时周期公式可近似表述为T=2π(1+$\frac{1}{4}$sin2$\frac{θ}{2}$)$\sqrt{\frac{l}{g}}$.为了用图象法验证单摆周期T和最大摆角θ的关系,他测出摆长为l的同一单摆在不同最大摆角θ时的周期T,并根据实验数据描绘出如图2所示的图线.根据所给周期公式可知,图中的纵轴表示的是sin2$\frac{θ}{2}$,图线延长后与横轴交点的横坐标为$2π\sqrt{\frac{l}{g}}$.
16.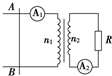 如图所示,理想变压器原、副线圈匝数之比n1:n2=4:1,原线圈两端连接光滑导轨,副线圈与电阻R相连组成闭合回路.当直导线AB在匀强磁场中沿导轨匀速地向左做切割磁感线运动时,安培表A1的读数是12mA,那么安培表A2的读数是( )
如图所示,理想变压器原、副线圈匝数之比n1:n2=4:1,原线圈两端连接光滑导轨,副线圈与电阻R相连组成闭合回路.当直导线AB在匀强磁场中沿导轨匀速地向左做切割磁感线运动时,安培表A1的读数是12mA,那么安培表A2的读数是( )
 如图所示,理想变压器原、副线圈匝数之比n1:n2=4:1,原线圈两端连接光滑导轨,副线圈与电阻R相连组成闭合回路.当直导线AB在匀强磁场中沿导轨匀速地向左做切割磁感线运动时,安培表A1的读数是12mA,那么安培表A2的读数是( )
如图所示,理想变压器原、副线圈匝数之比n1:n2=4:1,原线圈两端连接光滑导轨,副线圈与电阻R相连组成闭合回路.当直导线AB在匀强磁场中沿导轨匀速地向左做切割磁感线运动时,安培表A1的读数是12mA,那么安培表A2的读数是( )| A. | 0 | B. | 3mA | C. | 48 mA | D. | 无法确定 |
11.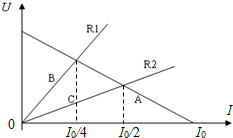 如图所示,直线A是电源的路端电压和电流的关系图线,直线B、C分别是电阻R1、R2的两端电压与电流的关系图线,若这两个电阻分别接到这个电源上,则( )
如图所示,直线A是电源的路端电压和电流的关系图线,直线B、C分别是电阻R1、R2的两端电压与电流的关系图线,若这两个电阻分别接到这个电源上,则( )
 如图所示,直线A是电源的路端电压和电流的关系图线,直线B、C分别是电阻R1、R2的两端电压与电流的关系图线,若这两个电阻分别接到这个电源上,则( )
如图所示,直线A是电源的路端电压和电流的关系图线,直线B、C分别是电阻R1、R2的两端电压与电流的关系图线,若这两个电阻分别接到这个电源上,则( )| A. | R1接在电源上时,电源的效率高 | |
| B. | R2接在电源上时,电源的效率高 | |
| C. | R1接在电源上时,电源的输出功率大 | |
| D. | 电源的输出功率一样大 |
 如图所示,活塞的质量为m,缸套的质量为M,通过弹簧吊在天花板上,汽缸内封住一定质量的气体,缸套和活塞间无摩擦,活塞面积为S,大气压强为p0,则封闭气体的压强为P0-$\frac{Mg}{S}$,若外界大气压减小,则活塞将不动,气缸将下降(上升或下降或不动)
如图所示,活塞的质量为m,缸套的质量为M,通过弹簧吊在天花板上,汽缸内封住一定质量的气体,缸套和活塞间无摩擦,活塞面积为S,大气压强为p0,则封闭气体的压强为P0-$\frac{Mg}{S}$,若外界大气压减小,则活塞将不动,气缸将下降(上升或下降或不动)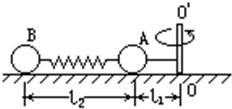 A、B两球质量分别为m1与m2,用一劲度系数为K的弹簧相连,一长为L1的细线与m1相连,置于水平光滑桌面上,细线的另一端拴在竖直轴OO′上,如图所示,当m1与m2均以角速度ω绕OO′做匀速圆周运动时,弹簧长度为L2.求:
A、B两球质量分别为m1与m2,用一劲度系数为K的弹簧相连,一长为L1的细线与m1相连,置于水平光滑桌面上,细线的另一端拴在竖直轴OO′上,如图所示,当m1与m2均以角速度ω绕OO′做匀速圆周运动时,弹簧长度为L2.求: