题目内容
13.光滑水平面上质量m=2kg的滑块A以v=3m/s的速度碰撞质量为4kg的静止滑块B,在B靠近A的一侧安装一轻弹簧,问:(1)当碰撞后A以1m/s的速度反向运动时,滑块B的速度为多少?
(2)在碰撞过程中弹簧具有的最大的弹性势能是多大?
分析 (1)由动量守恒定律可以求出碰撞后物体的速度;
(2)A、B速度相等时,弹簧的弹性势能最大,由动量守恒定律与能量守恒定律可以求出最大弹性势能.
解答 解:(1)碰撞过程动量守恒,以A的初速度方向为正方向,由动量守恒定律得:
mAv=-mAvA+mBvB,
即:2×3=-2×1+4vB,
解得:vB=2m/s
(2)A、B共速时,弹簧的弹性势能最大,A、B碰撞过程动量守恒,以A的初速度方向为正方向,
由动量守恒定律得:mAv=(mA+mB)v′,
由机械能守恒定律得:$△{E}_{P}=\frac{1}{2}{m}_{A}{{v}_{\;}}^{2}-\frac{1}{2}({m}_{A}+{m}_{B})v{′}^{2}$,
代入数据得:△EP=6J;
答:(1)当碰撞后A以1m/s的速度反向运动时,滑块B的速度为2m/s;
(2)在碰撞过程中弹簧具有的最大的弹性势能是6J.
点评 本题考查了求弹簧的弹性势能、B的速度,分析清楚物体运动过程是正确解题的前提与关键,应用动量守恒定律与机械能守恒定律即可正确解题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.边长为a的正方形的四个顶点上放置如图所示的点电荷,则中心O处场强( )


| A. | 大小为零 | B. | 大小为$\frac{\sqrt{2}kq}{{a}^{2}}$方向沿x轴正向 | ||
| C. | 大小为$\frac{2\sqrt{2}kq}{{a}^{2}}$方向沿y轴正向 | D. | 大小为$\frac{\sqrt{2}kq}{2{a}^{2}}$方向沿y轴负向 |
4.物理学的发展离不开许多物理学家的智慧和奋斗,我们学习物理知识的同时也要学习他们的精神,记住他们的贡献.关于他们的贡献,以下说法正确的是( )
| A. | 爱因斯坦通过实验发现通电导线周围存在磁场,并提出了判断磁场方向的左手定则 | |
| B. | 奥斯特通过近十年的艰苦探索终于发现了“磁生电”的规律 | |
| C. | 法拉第通过实验发现了电磁感应现象,并总结出了感应电流方向的判断方法 | |
| D. | 变化的磁场能够在周围空间产生电场,是麦克斯韦最先提出的基本假设之一 |
8. 欧姆最早是用小磁针测量电流的,他的具体做法是将一个小磁针处于水平静止状态,在其上方平行于小磁针放置一通电长直导线,已知导线外某磁感应强度与电流成正比,当导线中通有电流时,小磁针会发生偏转,通过小磁针偏转的角度可测量导线中电流.小磁针转动平面的俯视图如图所示.关于这种测量电流的方法,下列叙述正确的是( )
欧姆最早是用小磁针测量电流的,他的具体做法是将一个小磁针处于水平静止状态,在其上方平行于小磁针放置一通电长直导线,已知导线外某磁感应强度与电流成正比,当导线中通有电流时,小磁针会发生偏转,通过小磁针偏转的角度可测量导线中电流.小磁针转动平面的俯视图如图所示.关于这种测量电流的方法,下列叙述正确的是( )
 欧姆最早是用小磁针测量电流的,他的具体做法是将一个小磁针处于水平静止状态,在其上方平行于小磁针放置一通电长直导线,已知导线外某磁感应强度与电流成正比,当导线中通有电流时,小磁针会发生偏转,通过小磁针偏转的角度可测量导线中电流.小磁针转动平面的俯视图如图所示.关于这种测量电流的方法,下列叙述正确的是( )
欧姆最早是用小磁针测量电流的,他的具体做法是将一个小磁针处于水平静止状态,在其上方平行于小磁针放置一通电长直导线,已知导线外某磁感应强度与电流成正比,当导线中通有电流时,小磁针会发生偏转,通过小磁针偏转的角度可测量导线中电流.小磁针转动平面的俯视图如图所示.关于这种测量电流的方法,下列叙述正确的是( )| A. | 导线中电流的大小与小磁针转过的角度成正比 | |
| B. | 通电后小磁针静止时N极所指的方向是电流产生磁场的方向 | |
| C. | 若将导线垂直于小磁针放置,则不能完成测量 | |
| D. | 这种方法只能测量电流的大小,不能测量电流的方向 |
18.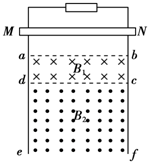 如图所示,光滑的“Π”形金属导体框竖直放置,质量为m的金属棒MN与框架接触良好,磁感应强度分别为B1、B2的有界匀强磁场方向相反,但均垂直于框架平面,分别处在abcd和cdef区域.现从图示位置由静止释放金属棒MN,金属棒进入磁场区域abcd后恰好做匀速运动.下列说法正确的有( )
如图所示,光滑的“Π”形金属导体框竖直放置,质量为m的金属棒MN与框架接触良好,磁感应强度分别为B1、B2的有界匀强磁场方向相反,但均垂直于框架平面,分别处在abcd和cdef区域.现从图示位置由静止释放金属棒MN,金属棒进入磁场区域abcd后恰好做匀速运动.下列说法正确的有( )
 如图所示,光滑的“Π”形金属导体框竖直放置,质量为m的金属棒MN与框架接触良好,磁感应强度分别为B1、B2的有界匀强磁场方向相反,但均垂直于框架平面,分别处在abcd和cdef区域.现从图示位置由静止释放金属棒MN,金属棒进入磁场区域abcd后恰好做匀速运动.下列说法正确的有( )
如图所示,光滑的“Π”形金属导体框竖直放置,质量为m的金属棒MN与框架接触良好,磁感应强度分别为B1、B2的有界匀强磁场方向相反,但均垂直于框架平面,分别处在abcd和cdef区域.现从图示位置由静止释放金属棒MN,金属棒进入磁场区域abcd后恰好做匀速运动.下列说法正确的有( )| A. | 若B2=B1,则金属棒进入cdef区域后将加速下滑 | |
| B. | 若B2=B1,则金属棒进入cdef区域后仍将保持匀速下滑 | |
| C. | 若B2<B1,则金属棒进入cdef区域后可能先加速后匀速下滑 | |
| D. | 若B2>B1,则金属棒进入cdef区域后可能先加速后匀速下滑 |
5.汽车A在红绿灯前停住,绿灯亮起时起动,以0.4m/s2的加速度做匀加速运动,经过30s后以该时刻的速度做匀速直线运动.设在绿灯亮的同时,汽车B以8m/s的速度从A车旁边驶过,且一直以相同的速度做匀速直线运动,运动方向与A车相同,则从绿灯亮时开始( )
| A. | A车在加速过程中与B车相遇? | B. | A、B相遇时速度相同? | ||
| C. | 相遇时A车做匀速运动? | D. | 两车可能再次相遇? |
2.一弹簧振子振动过程中的某段时间内其加速度数值越来越大,则在这段时间内( )
| A. | 振子的速度越来越大 | |
| B. | 振子正在向平衡位置运动 | |
| C. | 振子的速度方向与加速度方向一定相同 | |
| D. | 以上说法都不正确 |
3.在下列四个核反应方程中,符号“X”表示中子的是( )
| A. | ${\;}_{13}^{27}$Al+${\;}_{0}^{1}$n→${\;}_{12}^{27}$Mg+X | B. | ${\;}_{11}^{24}$Na→${\;}_{12}^{24}$Mg+X | ||
| C. | ${\;}_{4}^{9}$Be+${\;}_{2}^{4}$He→${\;}_{6}^{12}$C+X | D. | ${\;}_{52}^{239}$U→${\;}_{93}^{239}$Np+X |
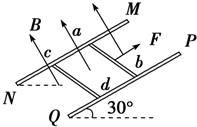 如图所示,两根足够长的光滑平行金属导轨MN、PQ间距为L=0.5m,其电阻不计,两导轨及其构成的平面与水平面成30°角.完全相同的两金属棒ab、cd分别垂直导轨放置,每棒两端都与导轨始终良好接触,已知两棒质量均为m=0.02kg,电阻均为R=0.1Ω,整个装置处在垂直于导轨平面向上的匀强磁场中,磁感应强度B=0.2T,棒ab在平行于导轨向上的力F作用下,沿导轨向上匀速运动,而棒cd恰好能够保持静止.g取10m/s2,
如图所示,两根足够长的光滑平行金属导轨MN、PQ间距为L=0.5m,其电阻不计,两导轨及其构成的平面与水平面成30°角.完全相同的两金属棒ab、cd分别垂直导轨放置,每棒两端都与导轨始终良好接触,已知两棒质量均为m=0.02kg,电阻均为R=0.1Ω,整个装置处在垂直于导轨平面向上的匀强磁场中,磁感应强度B=0.2T,棒ab在平行于导轨向上的力F作用下,沿导轨向上匀速运动,而棒cd恰好能够保持静止.g取10m/s2,