题目内容
10.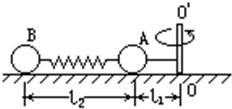 A、B两球质量分别为m1与m2,用一劲度系数为K的弹簧相连,一长为L1的细线与m1相连,置于水平光滑桌面上,细线的另一端拴在竖直轴OO′上,如图所示,当m1与m2均以角速度ω绕OO′做匀速圆周运动时,弹簧长度为L2.求:
A、B两球质量分别为m1与m2,用一劲度系数为K的弹簧相连,一长为L1的细线与m1相连,置于水平光滑桌面上,细线的另一端拴在竖直轴OO′上,如图所示,当m1与m2均以角速度ω绕OO′做匀速圆周运动时,弹簧长度为L2.求:(1)此时弹簧伸长量多大;
(2)绳子张力多大;
(3)将线突然烧断瞬间两球加速度各多大?
分析 (1、2)B球绕OO′做匀速圆周运动,靠弹簧的弹力提供向心力,求出弹簧的弹力,根据胡克定律即可得出弹簧的伸长量.A球在水平方向上受绳子的拉力和弹簧的弹力,两个力合力提供A球做圆周运动的向心力,从而求出绳子的拉力.
(3)绳子突然烧断的瞬间,绳子拉力立即消失,弹簧的弹力来不及发生变化,根据牛顿第二定律分别求出A球的合力,从而得出A球的加速度.
解答 解:(1)对B球有:F=m2(L1+L2)ω 2,
又根据胡克定律得:F=kx
所以弹簧的形变量:x=$\frac{F}{K}$=$\frac{{{m}_{2}({{L}_{1}+L}_{2})ω}^{2}}{K}$;
(2)根据牛顿第二定律有,对A球有:T-F=${{{m}_{1}L}_{1}ω}^{2}$
解得:T=[m2L2+(m1+m2)L1]ω2.
(3)烧断细绳的瞬间,拉力T=0,弹力F不变
根据牛顿第二定律,对A球有:aA=$\frac{F}{{m}_{1}}$=$\frac{{{m}_{2}({{L}_{1}+L}_{2})ω}^{2}}{{m}_{1}}$.
对B球有:aB=$\frac{F}{{m}_{2}}$=ω2(L1+L2)
答:(1)弹簧的形变量为$\frac{{{m}_{2}({{L}_{1}+L}_{2})ω}^{2}}{K}$;
(2)绳子张力为[m2L2+(m1+m2)L1]ω2;
(3)线突然烧断瞬间A球的加速度大小为$\frac{{{m}_{2}({{L}_{1}+L}_{2})ω}^{2}}{{m}_{1}}$,B球的加速度大小是ω2(L1+L2).
点评 解决本题的关键知道匀速圆周运动的向心力靠合力提供,以及知道在烧断细绳的瞬间,拉力立即消失,弹簧的弹力来不及改变,烧断细绳的前后瞬间弹力不变.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案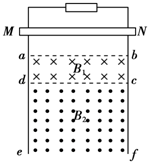 如图所示,光滑的“Π”形金属导体框竖直放置,质量为m的金属棒MN与框架接触良好,磁感应强度分别为B1、B2的有界匀强磁场方向相反,但均垂直于框架平面,分别处在abcd和cdef区域.现从图示位置由静止释放金属棒MN,金属棒进入磁场区域abcd后恰好做匀速运动.下列说法正确的有( )
如图所示,光滑的“Π”形金属导体框竖直放置,质量为m的金属棒MN与框架接触良好,磁感应强度分别为B1、B2的有界匀强磁场方向相反,但均垂直于框架平面,分别处在abcd和cdef区域.现从图示位置由静止释放金属棒MN,金属棒进入磁场区域abcd后恰好做匀速运动.下列说法正确的有( )| A. | 若B2=B1,则金属棒进入cdef区域后将加速下滑 | |
| B. | 若B2=B1,则金属棒进入cdef区域后仍将保持匀速下滑 | |
| C. | 若B2<B1,则金属棒进入cdef区域后可能先加速后匀速下滑 | |
| D. | 若B2>B1,则金属棒进入cdef区域后可能先加速后匀速下滑 |
| A. | A车在加速过程中与B车相遇? | B. | A、B相遇时速度相同? | ||
| C. | 相遇时A车做匀速运动? | D. | 两车可能再次相遇? |
| A. | 300W | B. | 400W | C. | 500W | D. | 700W |
| A. | 振子的速度越来越大 | |
| B. | 振子正在向平衡位置运动 | |
| C. | 振子的速度方向与加速度方向一定相同 | |
| D. | 以上说法都不正确 |
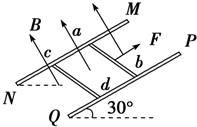 如图所示,两根足够长的光滑平行金属导轨MN、PQ间距为L=0.5m,其电阻不计,两导轨及其构成的平面与水平面成30°角.完全相同的两金属棒ab、cd分别垂直导轨放置,每棒两端都与导轨始终良好接触,已知两棒质量均为m=0.02kg,电阻均为R=0.1Ω,整个装置处在垂直于导轨平面向上的匀强磁场中,磁感应强度B=0.2T,棒ab在平行于导轨向上的力F作用下,沿导轨向上匀速运动,而棒cd恰好能够保持静止.g取10m/s2,
如图所示,两根足够长的光滑平行金属导轨MN、PQ间距为L=0.5m,其电阻不计,两导轨及其构成的平面与水平面成30°角.完全相同的两金属棒ab、cd分别垂直导轨放置,每棒两端都与导轨始终良好接触,已知两棒质量均为m=0.02kg,电阻均为R=0.1Ω,整个装置处在垂直于导轨平面向上的匀强磁场中,磁感应强度B=0.2T,棒ab在平行于导轨向上的力F作用下,沿导轨向上匀速运动,而棒cd恰好能够保持静止.g取10m/s2,