题目内容
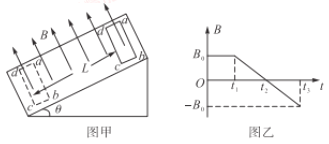
【题目】如图所示，在倾角θ=30的足够长斜面上放置一长木板，长木板质量M=3.0 kg，其上表面光滑，下表面粗糙，木板的下端有一个凸起的挡板，木板处于静止状态。将质量为m=1.0 kg的小物块放置在木板上，从距离挡板L=1.6m处由静止开始释放。物块下滑后与挡板相撞，撞击时间极短，相撞后瞬间物块的速率为
=2.0 m/s.木板开始下滑，且当木板沿斜面下滑至速度为零时，物块与木板恰好发生第二次相撞。取重力加速度g=10m/s.求：
(1)物块与木板第一次相撞后瞬间木板的速率；
(2)长木板与斜面之间的动摩擦因数μ. (计算结果保留两位有效数字)
【答案】(1) 2.0 m/s (2) 
【解析】(1)物块下滑的加速度a=gsin30=5.0m/s
物块第一次下滑至挡板时的速度
经分析可知，物块与挡板第一次相撞后反弹，由动量守恒定律可得
解得
=2.0 m/s
(2)设木板下滑的加速度为a′，由题中条件可得
解得
由牛顿第二运动定律可得
解得
练习册系列答案
名校课堂系列答案
相关题目
