题目内容
4. 如图甲为一列沿x轴传播的简谐波在t=O.1s时刻的波形图,图乙表示该波传播的介质中x=2m处的质点a从t=0时起的振动图象.则( )
如图甲为一列沿x轴传播的简谐波在t=O.1s时刻的波形图,图乙表示该波传播的介质中x=2m处的质点a从t=0时起的振动图象.则( )| A. | 波传播的速度为20m/s | |
| B. | 波沿x轴正方向传播 | |
| C. | 波沿x轴负方向传播 | |
| D. | t=0.15s时,质点a的加速度沿y轴负方向 | |
| E. | t=0.15s时,x=4m处的质点b的加速度沿y轴正方向 |
分析 本题要在乙图上读出a质点在t=0时刻的速度方向,在甲图上判断出波的传播度方向;由甲图读出波长,由乙图读出周期,即求出波速和频率.
解答 解:A、由甲图知,波长λ=4m,由乙图知,质点的振动周期为T=0.2s,则波速为:v$\frac{λ}{T}$=20m/s.故A正确;
BC、由乙图知,t=0.1s时刻,质点a正向上运动,根据甲图可知,该波沿x轴负方向传播,故B错误,C正确;
D、由乙图知,质点a在t=0.15s时刻处于正向最大位移处,所以a的加速度沿y轴负方向.故D正确;
E、t=O.1s时刻,x=4m处的质点b正通过平衡位置向下运动,再过$\frac{T}{4}$=0.5s,即t=0.15s时b到达波谷,则质点b的加速度沿y轴正方向.故E正确.
故选:ACDE.
点评 本题关键要把握两种图象的联系,能根据振动图象读出质点的速度方向,在波动图象上判断出波的传播方向,注意判断方法的不同,不能混淆.

练习册系列答案
相关题目
15.一辆卡车以15m/s的速度匀速行驶,司机突然发现正前方十字路口处有一个小孩跌倒在地,该司机刹车的反应时间为0.6s,刹车后卡车匀减速前进,最后停在小孩前1.5m处.已知刹车过程中卡车加速度的大小为5m/s2,则( )
| A. | 司机发现情况时,卡车与该小孩的距离为33m | |
| B. | 司机发现情况时,卡车与该小孩的距离为31.5 m | |
| C. | 司机发现情况后,卡车经过3.6s停下 | |
| D. | 司机发现情况后,卡车经过3s停下 |
19. 半径为r的带缺口的刚性金属圆环在纸面上固定放置,在圆环的缺口两端引出两根导线,分别与两块垂直于纸面固定放置的平行金属板连接,两板间距为d,如图甲所示.圆环内有一变化的磁场垂直于纸面,规定垂直纸面向里的方向为正,变化规律如图乙所示.在t=0时刻平行板之间的中心位置有一电荷量为+q的粒子由静止释放,粒子的重力不计,平行板电容器的充、放电时间不计,取上板的电势为零.则以下说法中正确的是( )
半径为r的带缺口的刚性金属圆环在纸面上固定放置,在圆环的缺口两端引出两根导线,分别与两块垂直于纸面固定放置的平行金属板连接,两板间距为d,如图甲所示.圆环内有一变化的磁场垂直于纸面,规定垂直纸面向里的方向为正,变化规律如图乙所示.在t=0时刻平行板之间的中心位置有一电荷量为+q的粒子由静止释放,粒子的重力不计,平行板电容器的充、放电时间不计,取上板的电势为零.则以下说法中正确的是( )
 半径为r的带缺口的刚性金属圆环在纸面上固定放置,在圆环的缺口两端引出两根导线,分别与两块垂直于纸面固定放置的平行金属板连接,两板间距为d,如图甲所示.圆环内有一变化的磁场垂直于纸面,规定垂直纸面向里的方向为正,变化规律如图乙所示.在t=0时刻平行板之间的中心位置有一电荷量为+q的粒子由静止释放,粒子的重力不计,平行板电容器的充、放电时间不计,取上板的电势为零.则以下说法中正确的是( )
半径为r的带缺口的刚性金属圆环在纸面上固定放置,在圆环的缺口两端引出两根导线,分别与两块垂直于纸面固定放置的平行金属板连接,两板间距为d,如图甲所示.圆环内有一变化的磁场垂直于纸面,规定垂直纸面向里的方向为正,变化规律如图乙所示.在t=0时刻平行板之间的中心位置有一电荷量为+q的粒子由静止释放,粒子的重力不计,平行板电容器的充、放电时间不计,取上板的电势为零.则以下说法中正确的是( )| A. | 第2s末粒子回到了原来位置 | |
| B. | 第3s内上极板为正极 | |
| C. | 第2s末两极板之间的电场强度大小为$\frac{π{r}^{2}}{10d}$(V/m) | |
| D. | t=3.4s时,下极板的电势为$\frac{π{r}^{2}}{20}$(V) |
9. 某物体放在粗糙的水平面上,初速为零,第一次用力F推,第二次用力F拉,如图所示:两次θ角、力F大小和物体位移S都相同,那么( )
某物体放在粗糙的水平面上,初速为零,第一次用力F推,第二次用力F拉,如图所示:两次θ角、力F大小和物体位移S都相同,那么( )
 某物体放在粗糙的水平面上,初速为零,第一次用力F推,第二次用力F拉,如图所示:两次θ角、力F大小和物体位移S都相同,那么( )
某物体放在粗糙的水平面上,初速为零,第一次用力F推,第二次用力F拉,如图所示:两次θ角、力F大小和物体位移S都相同,那么( )| A. | 第一次力F对物体做功多 | B. | 第二次力F对物体做功多 | ||
| C. | 两次力F对物体做功一样多 | D. | 无法比较哪一次力F做功多 |
16. 如图所示为游乐场中滑梯示意图,小孩从轨道顶端由静止开始下滑,沿水平轨道滑动了一段距离后停下,则下滑过程中( )
如图所示为游乐场中滑梯示意图,小孩从轨道顶端由静止开始下滑,沿水平轨道滑动了一段距离后停下,则下滑过程中( )
 如图所示为游乐场中滑梯示意图,小孩从轨道顶端由静止开始下滑,沿水平轨道滑动了一段距离后停下,则下滑过程中( )
如图所示为游乐场中滑梯示意图,小孩从轨道顶端由静止开始下滑,沿水平轨道滑动了一段距离后停下,则下滑过程中( )| A. | 小孩的重力势能增加 | B. | 支持力对小孩不做功 | ||
| C. | 摩擦力对小孩先做正功后做负功 | D. | 小孩的机械能守恒 |
13.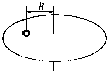 安徽电视台《男生女生向前冲》的节目里,一位选手在转盘上随转盘一起做匀速圆周运动,转速为n.如果选手可视为质点,其质量为m,选手到转轴的距离为R,与转盘间的动摩擦因数为μ,滑动摩擦力等于最大静摩擦力,重力加速度为g,则( )
安徽电视台《男生女生向前冲》的节目里,一位选手在转盘上随转盘一起做匀速圆周运动,转速为n.如果选手可视为质点,其质量为m,选手到转轴的距离为R,与转盘间的动摩擦因数为μ,滑动摩擦力等于最大静摩擦力,重力加速度为g,则( )
 安徽电视台《男生女生向前冲》的节目里,一位选手在转盘上随转盘一起做匀速圆周运动,转速为n.如果选手可视为质点,其质量为m,选手到转轴的距离为R,与转盘间的动摩擦因数为μ,滑动摩擦力等于最大静摩擦力,重力加速度为g,则( )
安徽电视台《男生女生向前冲》的节目里,一位选手在转盘上随转盘一起做匀速圆周运动,转速为n.如果选手可视为质点,其质量为m,选手到转轴的距离为R,与转盘间的动摩擦因数为μ,滑动摩擦力等于最大静摩擦力,重力加速度为g,则( )| A. | 选手的线速度v=$\frac{R}{n}$ | |
| B. | 选手的角速度ω=$\frac{2π}{n}$ | |
| C. | 选手的向心加速度an=4π2n2R | |
| D. | 选手相对转盘打滑时的临界速度vm=$\sqrt{\frac{μg}{R}}$ |
14.月球的表面长期受到宇宙射线的照顾,使得“月壤”中的${\;}_{2}^{3}$He含量十分丰富,科学家认为${\;}_{2}^{3}$He是发生核聚变的极好原料,将来${\;}_{2}^{3}$He也许是人类重要的能源,所以探测月球意义十分重大.关于${\;}_{2}^{3}$He,下列说法正确的是( )
| A. | ${\;}_{2}^{3}$He的原子核内有三个中子和两个质子 | |
| B. | ${\;}_{2}^{3}$He的原子核内有一个中子和两个质子 | |
| C. | ${\;}_{2}^{3}$He发生和核聚变,放出热量,一定会有质量亏损 | |
| D. | ${\;}_{2}^{3}$He的原子核内的核子靠万有引力紧密结合在一起 | |
| E. | ${\;}_{2}^{3}$He的原子核与氘核聚变成${\;}_{2}^{4}$He的方程为:${\;}_{2}^{3}$He+${\;}_{1}^{2}$H→${\;}_{2}^{4}$He+${\;}_{1}^{1}$H |
 某物理兴趣小组采用如图所示的装置测平抛问题的初速度,A、B小球处于同一高度,M为A球中心初始时在水平地面上的垂直投影.用小锤打击弹性金属片,使小球沿水平方向飞出,同时松开B球,B球自由下落.A球落到地面N点处,B球落到地面P点处.测得B球距地面的高度是0.784m,M、N两点间的距离为1.2m,则B球落到P点的时间为0.4s,A球刚抛出时的速度为3m/s.(忽略空气阻力,g取9.8m/s2)
某物理兴趣小组采用如图所示的装置测平抛问题的初速度,A、B小球处于同一高度,M为A球中心初始时在水平地面上的垂直投影.用小锤打击弹性金属片,使小球沿水平方向飞出,同时松开B球,B球自由下落.A球落到地面N点处,B球落到地面P点处.测得B球距地面的高度是0.784m,M、N两点间的距离为1.2m,则B球落到P点的时间为0.4s,A球刚抛出时的速度为3m/s.(忽略空气阻力,g取9.8m/s2)