题目内容
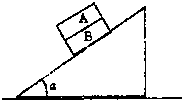
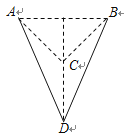
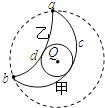
【题目】半径为a右端开小口的导体圆环和长为2a的导体直杆,单位长度电阻均为R0 . 圆环水平固定放置,整个内部区域分布着竖直向下的匀强磁场,磁感应强度为B.杆在圆环上以速度v平行于直径CD向右做匀速直线运动,杆始终有两点与圆环良好接触,从圆环中心O开始,杆的位置由θ确定,如图所示.则( )
A.θ=0时,杆产生的电动势为2Bav
B.θ= ![]() 时,杆产生的电动势为
时,杆产生的电动势为 ![]()
C.θ=0时,杆受的安培力大小为 ![]()
D.θ= ![]() 时,杆受的安培力大小为
时,杆受的安培力大小为 ![]()
【答案】A,D
【解析】解:A、θ=0时,杆产生的电动势E=BLv=2Bav,故A正确;
B、θ= ![]() 时,根据几何关系得出此时导体棒的有效切割长度是a,所以杆产生的电动势为Bav,故B错误;
时,根据几何关系得出此时导体棒的有效切割长度是a,所以杆产生的电动势为Bav,故B错误;
C、θ=0时,由于单位长度电阻均为R0.所以电路中总电阻(2+π/2)aR0.
所以杆受的安培力大小F=BIL=B2a ![]() =
= ![]() ,故C错误;
,故C错误;
D、θ= ![]() 时,电路中总电阻是(
时,电路中总电阻是( ![]() π+1)aR0
π+1)aR0
所以杆受的安培力大小F′=BI′L′= ![]() ,故D正确;
,故D正确;
故选:AD.
根据几何关系求出此时导体棒的有效切割长度,根据法拉第电磁感应定律求出电动势.
注意总电阻的求解,进一步求出电流值,即可算出安培力的大小.

【题目】在“用DIS研究在温度不变时,一定质量的气体压强与体积的关系”实验中,某同学将注射器活塞置于中间刻度20ml处,然后将注射器连接压强传感器并开始实验,气体体积V每减小2ml测一次压强p,实验数据记录在下表中最后得到p和V的乘积逐渐减小.
序号 | V(ml) | p(×105Pa) | pV(×105Paml) |
1 | 20.0 | 1.0010 | 20.020 |
2 | 18.0 | 1.0952 | 19.714 |
3 | 16.0 | 1.2313 | 19.701 |
4 | 14.0 | 1.4030 | 19.642 |
5 | 12.0 | 1.6351 | 19.621 |
(1)(单选题)造成上述实验结果的可能原因是在实验过程中
(A)注射器中有异物
(B)实验时环境温度增大了.
(C)实验时外界大气压强发生了变化.
(D)实验时注射器内的空气向外发生了泄漏.
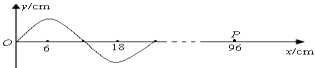
(2)由此可推断,该同学的实验结果可能为上图(选填“a”或“b”).
(3)若另一同学用较大的注射器在同一实验室里(温度不变)做同一个实验,实验仪器完好,操作规范,也从中间刻度开始实验,则得出的V﹣ ![]() 图象的斜率比上一同学直线部分的斜率相比(选填“增大”、“减小”或“相同”).
图象的斜率比上一同学直线部分的斜率相比(选填“增大”、“减小”或“相同”).