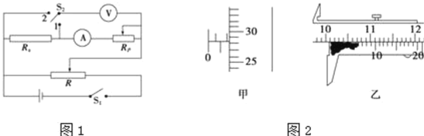
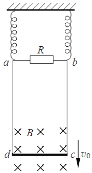
��Ŀ����
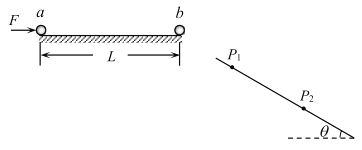
����Ŀ����ͼ������L=4.5m��ˮƽ�����������˸����ô�С��ͬ��С��a��b�����������·��ʵ�λ�÷��������=30����б�棬С��b������Ϊ0.3kgС��a�ں㶨ˮƽ����F��������a0=4m/s2�ļ��ٶ������˶�����С��a����Ҫ��С��b��ײʱ��ȥ����F����С����ײ��С��a�Ķ��ܼ���Ϊԭ�����ķ�֮һ���Ҹպ��ܷ��ص�������ˣ�С��b�䵽б���ϵ�P1�㣬��б����ײ��ˮƽ���ҷɳ���Ȼ���䵽б���ϵ�P2�㡣��֪С����б����ײǰ���ٶ���б��ļн���ȣ����������Ϊ�ʵ㣬��С�����ײ�Լ�С��b��б������ײ��Ϊ��ȫ������ײ������ײʱ�伫�̣��������ٶ�g=10m/s2����:
��1����С����ײ��С��a���ٶȴ�С��
��2������F�Ĵ�С��
��3��С��b��б���ϵ��������P1��P2��ľ��롣
���𰸡���1��![]() ����2��
����2��![]() ����3��
����3��![]()
��������
��1����С��a������Ϊ![]() ��С��b������Ϊ
��С��b������Ϊ![]() ����ײǰС��a���ٶ�
����ײǰС��a���ٶ�![]() ����ײ��С��a���ٶȴ�СΪ
����ײ��С��a���ٶȴ�СΪ![]() ��С��b���ٶȴ�СΪ
��С��b���ٶȴ�СΪ![]() ����
����
![]()
���
![]()
����
![]()
���
![]()
��2������ţ�ٵڶ�����
![]()
��ײ����
![]()
�����غ�
![]()
С��a���ع���
![]()
���
![]()
![]()
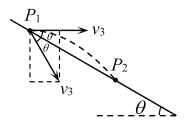
��3����ͼ��ʾ����С��b����б���ϵ�![]() ʱ���ٶȴ�СΪ
ʱ���ٶȴ�СΪ![]() ��
��![]() ��
��![]() �����Ϊ
�����Ϊ![]() ����
����![]() ��
��![]() ���˶�ʱ��Ϊt���ɼ��ι�ϵ��
���˶�ʱ��Ϊt���ɼ��ι�ϵ��
������ɵ�
![]()
С����ƽ���˶�
![]()
![]()
���
![]()