题目内容
【题目】如图，粗细均匀的均质杆AB在B点用铰链与竖直墙连接，杆长为L ． A端有一轻质滑轮（大小可忽略）．足够长的轻绳通过滑轮将重物吊住．若θ为370时恰好达到平衡，且保持绳AC在水平方向，则杆AB的质量m与重物的质量M的比值为 ． 若将杆换为长度不变的轻杆，其它条件不变，则系统平衡时轻杆与竖直墙面的夹角为 ． （sin37°=0.6，cos37°=0.8）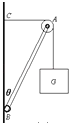
【答案】
；aRccos 
【解析】由于物体m受力平衡，故细线的拉力等于mg；
当若θ为37°时杆恰好达到平衡，以B为支点，设杆长为L ， 根据力矩平衡条件得：
sin37°+MgLsin37°=MgLcos37°
解得：m：M=2：3
设AB长为L ， 这BC为0.8L；
若将杆换为长度不变的轻杆，杆AB受到铰链的作用力和轻绳对AB的压力，要使杆能够平衡，轻绳对AB的压力方向应在AC与AB之间，而轻绳对AB的压力等于轻绳AC和AG拉力的合力，这两个拉力大小相等，故AB在细线的两侧拉力的角平分线上，如图所示：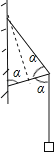
故
， 则α=aRccos
所以答案是： ，aRccos ．
练习册系列答案
相关题目
