题目内容
14.在用双缝干涉测光的波长的实验中,请按照题目要求回答下列问题.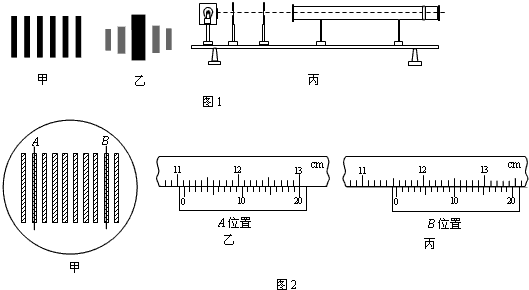
(1)如图1所示,甲、乙两图都是光的条纹形状示意图,其中干涉图样是甲.
(2)将下表中的光学元件放在图1的丙所示的光具座上组装成用双缝干涉测光的波长的实验装置,并用此装置测量红光的波长.
| 元件代号 | A | B | C | D | E |
| 元件名称 | 光屏 | 双缝 | 白光光源 | 单缝 | 透红光的 滤光片 |
(3)已知该装置中双缝间距d=0.50mm,双缝到光屏的距离l=0.50m,在光屏上得到的干涉图样如图2甲所示,分划板在图中A位置时游标卡尺如图2乙所示,则其示数xA=111.15 mm;在B位置时游标卡尺如图2丙所示,则相邻两条纹间距△x=0.64 mm;
(4)由以上所测数据,可以得出形成此干涉图样的单色光的波长为6.4×10-7 m.
(5)若改用频率较高的单色光照射,得到的干涉条纹间距将变小(填“变大”、“不变”或“变小”).
分析 (1)双缝干涉条纹特点是等间距、等宽度、等亮度;
(2)为获取单色线光源,白色光源后面要有滤光片、单缝、双缝,最后面是光屏;
(3)游标卡尺读数=可动刻度读数+游标尺读数;根据△x=xB−xA7xB−xA7 求出相邻亮纹的间距;根据△x=LdLdλ求解波长.
(5)根据双缝干涉条纹的间距公式△x=LdLdλ判断干涉条纹的间距变化.
解答 解:(1)双缝干涉条纹特点是等间距、等宽度、等亮度;衍射条纹特点是中间宽两边窄、中间亮、两边暗,且不等间距;根据此特点知甲图是干涉条纹;
(2)为获取单色线光源,白色光源后面要有滤光片、单缝、双缝.所以各光学元件的字母排列顺序应为:EDBA;
(3、4)游标卡尺读数=可动刻度读数+游标尺读数;
故xA=111mm+0.05mm×3=111.15mm;
xB=115mm+0.05mm×12=115.60mm;
相邻亮纹的间距:
△x=xB−xA7xB−xA7=0.11560−0.1111570.11560−0.111157≈0.00064m=0.64mm;
根据公式△x=LdLdλ,有:
λ=△x•dL△x∙dL=0.64×10−3−3×0.5×10−30.50.64×10−3−3×0.5×10−30.5=6.4×10-7m
(5)根据双缝干涉条纹的间距公式△x=LdLdλ知,频率变高,波长变短,则干涉条纹间距变小;
故答案为:
(1)甲;(2)EDBA;(3)111.15,0.64 mm;
(4)6.4×10-7;(5)变小.
点评 本题关键是明确实验原理,体会实验步骤,最好亲手做实验;解决本题的关键掌握游标卡尺的读数方法,以及掌握双缝干涉条纹的间距公式△x=LdLdλ.

练习册系列答案
相关题目
2.下列是热学的有关知识,说法中正确的是( )
| A. | 布朗运动反映了微粒中分子运动的不规则性 | |
| B. | 对相同种类的物体,只要温度相同,分子的平均动能一定相同 | |
| C. | 分子间距增大时,分子间的引力增大而斥力减小 | |
| D. | 能量耗散现象是从能量转化的角度反映出自然界中的宏观过程具有方向性 |
19.一段均匀带电的半圆形细线在其圆心O处产生的场强为E,把细线分成等长的圆弧^ABˆAB,^BCˆBC,^CDˆCD 则圆弧^BCˆBC在圆心O处产生的场强为( )
| A. | E | B. | E2E2 | C. | E3E3 | D. | E4E4 |
3. 如图所示,光滑的水平面上静置质量为M=8kg的平板小车,在小车左端加一个由零逐渐增大的水平堆力F,一个大小不计、质量为m=2kg的小物块放在小车右端上面,小物块与小车间的动摩擦因数μ=0.2,小车足够长,重力加速度g取10m/s2,设最大静摩擦力等于滑动摩擦力,下列说法中正确的是( )
如图所示,光滑的水平面上静置质量为M=8kg的平板小车,在小车左端加一个由零逐渐增大的水平堆力F,一个大小不计、质量为m=2kg的小物块放在小车右端上面,小物块与小车间的动摩擦因数μ=0.2,小车足够长,重力加速度g取10m/s2,设最大静摩擦力等于滑动摩擦力,下列说法中正确的是( )
 如图所示,光滑的水平面上静置质量为M=8kg的平板小车,在小车左端加一个由零逐渐增大的水平堆力F,一个大小不计、质量为m=2kg的小物块放在小车右端上面,小物块与小车间的动摩擦因数μ=0.2,小车足够长,重力加速度g取10m/s2,设最大静摩擦力等于滑动摩擦力,下列说法中正确的是( )
如图所示,光滑的水平面上静置质量为M=8kg的平板小车,在小车左端加一个由零逐渐增大的水平堆力F,一个大小不计、质量为m=2kg的小物块放在小车右端上面,小物块与小车间的动摩擦因数μ=0.2,小车足够长,重力加速度g取10m/s2,设最大静摩擦力等于滑动摩擦力,下列说法中正确的是( )| A. | 当F增加到4N时,m相对M开始运动 | |
| B. | 当F增加到20N时,m相对M开始运动 | |
| C. | 当F=10N时,m对M有向左的2N的摩擦力 | |
| D. | 当F=10N时,m对M有向左的4N的摩擦力 |
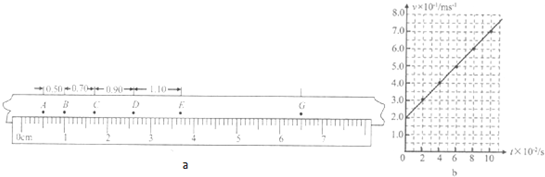
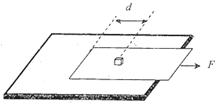 如图所示,将小物体(可视为质点)置于桌面上的簿纸板上,用水平向右的恒力F拉动纸板,拉力大小不同,纸板和小物体的运动情况也不同.若纸板的质量 m1=0.1kg,小物体的质量m2=0.4kg,小物体与纸板左边缘的距离d=0.09m,已知各接触面间的动摩擦因数均为μ=0.2,最大静摩擦力滑动摩擦力相等;g取10m/s2.求:
如图所示,将小物体(可视为质点)置于桌面上的簿纸板上,用水平向右的恒力F拉动纸板,拉力大小不同,纸板和小物体的运动情况也不同.若纸板的质量 m1=0.1kg,小物体的质量m2=0.4kg,小物体与纸板左边缘的距离d=0.09m,已知各接触面间的动摩擦因数均为μ=0.2,最大静摩擦力滑动摩擦力相等;g取10m/s2.求: 某同学做“验证力的平行四边形定则”实验的情况如图甲所示,其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳,图乙是在白纸上根据实验结果画出的图.
某同学做“验证力的平行四边形定则”实验的情况如图甲所示,其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳,图乙是在白纸上根据实验结果画出的图. 一列简谐横波在t=0时的波形图如图所示.介质中质点P沿y轴正方向做简谐运动,从此时开始10s内p点经过50次该位置.则此波沿x轴负(选填“正”或“负”)方向传播,传播速度为10m/s.
一列简谐横波在t=0时的波形图如图所示.介质中质点P沿y轴正方向做简谐运动,从此时开始10s内p点经过50次该位置.则此波沿x轴负(选填“正”或“负”)方向传播,传播速度为10m/s.