题目内容
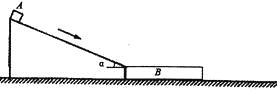
【题目】在一次低空跳伞演练中,当直升飞机悬停在离地面224m高处时,伞兵离开飞机做自由落体运动.运动一段时间后,打开降落伞,展伞后伞兵以12.5m/s2的加速度匀减速下降.为了伞兵的安全,要求伞兵落地速度最大不得超过5m/s,(取g=10m/s2)求:
(1)伞兵展伞时,离地面的高度至少为多少?着地时相当于从多高处自由落下?
(2)伞兵在空中的最短时间为多少?
【答案】
(1)解:设伞兵展伞时,离地面的高度至少为h,此时速度为v0,
则:
对于匀减速运动过程,有 ![]() ,
,
即52﹣ ![]() =﹣2×12.5×h
=﹣2×12.5×h
对于自由下落过程,有 ![]() =2g(224﹣h)=2×10×(224﹣h)
=2g(224﹣h)=2×10×(224﹣h)
联立解得h=99 m,v0=50 m/s
以5m/s的速度落地相当于从h1高处自由落下,
即2gh1=v2 所以h1= ![]() m=1.25 m.
m=1.25 m.
答:伞兵展伞时,离地面的高度至少为99m,着地时相当于从1.25m高处自由落下.
(2)解:设伞兵在空中的最短时间为t,
则有v0=gt1,
t1= ![]() s=5 s,
s=5 s,
t2= ![]() s=3.6 s,
s=3.6 s,
故所求时间t=t1+t2=(5+3.6)s=8.6 s.
答:伞兵在空中的最短时间为8.6s.
【解析】(1)整个过程中,伞兵先做自由落体运动,后做匀减速运动,总位移大小等于224m.设伞兵展伞时,离地面的高度至少为h,此时速度为v0,先研究匀减速过程,由速度﹣位移关系式,得到v0与h的关系式,再研究自由落体过程,也得到一个v0与h的关系式,联立求解.(2)由(1)求出v0,由速度公式求出两个过程的时间,即可得到总时间.
【考点精析】通过灵活运用自由落体运动,掌握(1)条件:初速度为零,只受重力作用;(2)性质:是一种初速为零的匀加速直线运动,a=g即可以解答此题.

 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案【题目】为了“探究加速度与力、质量的关系”,现提供如图甲所示的实验装置:

(1)以下实验操作正确的是
A.将木板不带滑轮的一端适当垫高,使小车在砝码及砝码盘的牵引下恰好做匀速运动 |
B.调节滑轮的高度,使细线与木板平行 |
C.先接通电源后释放小车 |
D.实验中小车的加速度越大越好 |
(2)在实验中,得到一条如图乙所示的纸带,已知相邻计数点间的时间间隔为T=0.1S,且间距x1、x2、x3、x4、x5、x6已量出分别为3.09cm、3.43cm、3.77cm、4.10cm、4.44cm、4.77cm,则小车的加速度a= m/s2(结果保留两位有效数字)。

(3)有一组同学保持小车及车中的砝码质量一定,探究加速度a与所受外力F的关系,他们在轨道水平及倾斜两种情况下分别做了实验,得到了两条a—F图线,如图丙所示。图线 是在轨道倾斜情况下得到的(填“①”或“②”);小车及车中砝码的总质量m= kg。