题目内容
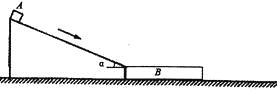
【题目】如图所示，一倾角a=37°、长度为9m的固定斜面，其底端与长木板B上表面等高．原来B静止在粗糙水平地面上，左端与斜面接触但不粘连，斜面底端与木板B的上表面接触处圆滑．一可视为质点的小滑块A从斜面顶端处由静止开始下滑，最终A刚好未从木板B上滑下．已知A、B的质量相等，木板B的长度L=3m,A与斜面、B上表面间的动摩擦因数均为μ1=0．5，B与地面的动摩擦因数为μ2，重力加速度g取10m／s2．
（1）通过计算分析当A滑上B的上表面后，B是否仍保持静止；
（2）若B仍然静止，求出μ2的最小值；若B滑动，求出μ2的值．
【答案】（1）B与地面会发生相对滑动
（2）0．2
【解析】试题分析：（1）设A物块从斜面下滑过程中加速度大小为a0，到达底端时速度大小为v0，由牛顿第二定律和运动学公式得：
①
②
由①②得： 
假设A滑上B的上表面后，B仍保持静止，则A在B上减速滑动至停止．
③
④
A会从B上滑下，假设不成立．
故当A滑上B的上表面后，B与地面会发生相对滑动．
（2）设A滑上B后，再经时间t两者达到共同速度，
A、B的加速度大小分别为：
⑤
⑥
⑦
⑧
⑨
解得: 
练习册系列答案
相关题目
