Question

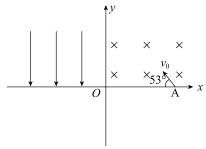
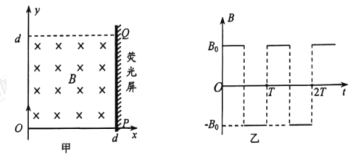
【题目】在如图甲所示的平面坐标系xOy内，正方形区域（0<x<d、0 <y<d）内存在垂直xOy平面周期性变化的匀强磁场，规定图示磁场方向为正方向，磁感应强度B的变化规律如图乙所示，变化的周期T可以调节，图中B0为己知。在x=d处放置一垂直于x轴的荧光屏，质量为m、电荷量为q的带负电粒子在t=0时刻从坐标原点O沿y轴正方向射入磁场，不计粒子重力。

（1）调节磁场的周期，满足T>，若粒子恰好打在屏上P（d，0）处，求粒子的速度大小v；

（2）调节磁场的周期，满足T=，若粒子恰好打在屏上Q（d，d）处，求粒子的加速度大小a；

（3）粒子速度大小为v0=时，欲使粒子垂直打到屏上，周期T应调为多大？

Answer 1

【答案】（1）；（2）(其中 k=1，2，3……)；（3）T=,其中sin=，=arcsin；sin=，=arcsin；sin=，=arcsin。

；

【解析】

（1）粒子的运动轨迹如图所示：

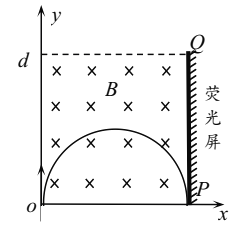
由洛伦兹力提供向心力，有：

qvB =m

几何关系可得：

2R1=d

联立解得：

（2）粒子的轨迹如图所示：

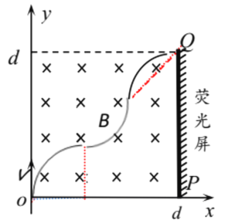
由几何关系可得：

，其中 k=1、2、3……

；

可得：

而

联立可得：

，其中k=1，2，3……

（3）洛伦兹力提供向心力，有：

qvB=m；

；

粒子运动轨迹如图所示，

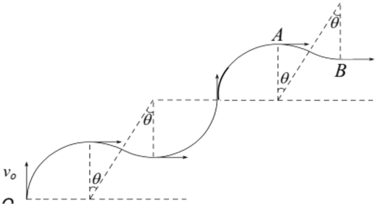
在每个磁感应强度变化的周期内，粒子在图示A、B两个位置可能垂直击中屏，且满足要求0<<。

设粒子运动的周期为T′，由题意得：

；

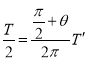设经历完整TB的个数为n （n = 0，1，2，3……）

（I）若粒子运动至A点击中屏，据题意由几何关系得：

R+2（R+Rsin）n=d

当 n=0、 1时无解；

当 n=2时，sin=，=arcsin；

n>2时无解。

（II）若粒子运动至B点击中屏，据题意由几何关系得:

R+2Rsin+2（R+Rsin）n=d

当n=0时无解。

n=1时，sin=，=arcsin；

n=2时：sin=，=arcsin；

n>2 时无解

综合得：

T= ；

其中sin=，=arcsin；sin=，=arcsin；sin=，=arcsin。