题目内容
【题目】科幻电影《流浪地球》中讲述了人类想方设法让地球脱离太阳系的故事。地球流浪途中在接近木星时被木星吸引，当地球快要撞击木星的危险时刻，点燃木星产生强大气流推开地球拯救了地球。若逃逸前，地球、木星沿各自的椭圆轨道绕太阳运行，且航天器在地球表面的重力为G1，在木星表面的重力为G2；地球与木星均可视为球体，其半径分别为R1、R2，则下列说法正确的是（ ）
A. 地球逃逸前，发射的航天器逃出太阳系的最小速度为
B. 木星与地球的第一宇宙速度之比为
C. 地球与木星绕太阳公转周期之比的立方等于它们轨道半长轴之比的平方
D. 地球与木星的质量之比为
【答案】D
【解析】
A．在地球的表面发射飞出太阳系的最小发射速度，叫做第三宇宙速度v3=16.7km/s，故A错误；
B．根据重力提供向心力得
，解得：地球上的第一宇宙速度
，同理得：木星上的第一宇宙速度为：
，故木星与地球的第一宇宙速度之比
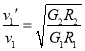，故B错误；
C．根据开普勒第三定律得：
，故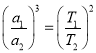
，即地球与木星绕太阳公转周期之比的平方等于它们轨道半长轴之比的三次方，故C错误；
D．根据重力与万有引力相等，
，解得：
，同理可得木星质量：
，故
，故D正确；
练习册系列答案
芝麻开花课程新体验系列答案
怎样学好牛津英语系列答案
相关题目
