题目内容
8. 如图所示,半径为r、圆心为O1的圆形区域内存在垂直纸面向外的匀强磁场,在磁场右侧有竖直放置的平行金属板M和N,两板间距离为L,在M、N板中央各有一个小孔02、O3,O1,O2,O3在同一水平直线上,与平行金属板相接的是两条竖直放置间距为L的足够长的光滑金属导轨,导体棒PQ与导轨接触良好,与阻值为R的电阻形成闭合回路(导轨与导体棒的电阻不计),该回路处在磁感应强度大小为B,方向垂直纸面向里的匀强磁场中,整个装置处在真空室中,有一束电荷量为+q、质量为m的粒子流(不计重力及粒子间相互作用),以速率v0从圆形磁场边界上点E沿半径方向射入圆形磁场区域,最后从小孔O3射出.∠EO1O2=120°.现释放导体棒PQ,其下滑h后开始匀速运动,此后从E点射入的粒子恰好不能从O3射出,而从圆形磁场的F点射出,已知∠FO1O2=120°求:
如图所示,半径为r、圆心为O1的圆形区域内存在垂直纸面向外的匀强磁场,在磁场右侧有竖直放置的平行金属板M和N,两板间距离为L,在M、N板中央各有一个小孔02、O3,O1,O2,O3在同一水平直线上,与平行金属板相接的是两条竖直放置间距为L的足够长的光滑金属导轨,导体棒PQ与导轨接触良好,与阻值为R的电阻形成闭合回路(导轨与导体棒的电阻不计),该回路处在磁感应强度大小为B,方向垂直纸面向里的匀强磁场中,整个装置处在真空室中,有一束电荷量为+q、质量为m的粒子流(不计重力及粒子间相互作用),以速率v0从圆形磁场边界上点E沿半径方向射入圆形磁场区域,最后从小孔O3射出.∠EO1O2=120°.现释放导体棒PQ,其下滑h后开始匀速运动,此后从E点射入的粒子恰好不能从O3射出,而从圆形磁场的F点射出,已知∠FO1O2=120°求:(1)棒下落h的整个过程中,电阻上产生的电热.
(2)粒子从E点到F点所用的时间.
分析 (1)粒子恰好不能从O3射出时,到达O3速度为零.根据动能定理求出此时板间电压,由平衡条件求出质量M.能量守恒定律求得电阻上产生的电热.
(2)粒子从E射入圆形磁场区域,从小孔O3射出,在磁场中做匀速圆周运动,由几何知识求出半径,再由牛顿定律求出B.根据轨迹,逐段求出时间,再求总时间.
解答 解:(1)设PQ棒匀速下滑时棒的速度为v,此时MN板间的电压为U,由题意有:
$\frac{1}{2}m{v}_{0}^{2}$=qU
解得U=$\frac{m{v}_{0}^{2}}{2q}$
由力平衡得 Mg=B$\frac{U}{R}L$
解得M=$\frac{BLm}{2gqR}{v}_{0}^{2}$
MN之间的电压:U=E=BLv
由能量守恒:Mgh=$\frac{1}{2}$Mv2+QR
联立上述方程解得产生的电热:QR=$\frac{BLmh}{2qR}{v}_{0}^{2}$-$\frac{{m}^{3}{v}_{0}^{6}}{16gBLR{q}^{3}}$
(2)粒子由E到O2过程中作半径为r的匀速圆周运动,∠EO1O2=120°则粒子的偏转角为60°,粒子运动的半径:$R=\frac{r}{tan30°}=\sqrt{3}r$
qvB=m$\frac{{v}_{0}^{2}}{R}$
解得B′=$\frac{m{v}_{0}}{\sqrt{3}qr}$
粒子后来从O3返回O2,进入磁场后在偏转60°从F点射出. 设粒子在圆形磁场内的运动时间t1:t1=$\frac{T}{6}+\frac{T}{6}$
周期:$T=\frac{2πR}{qB′}$
整理得:${t}_{1}=\frac{2\sqrt{3}πr}{3{v}_{0}}$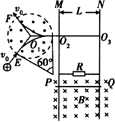
粒子在电场中往返运动的时间t2:由 L=$\frac{{0+v}_{0}}{2}•\frac{{t}_{2}}{2}$ 得 ${t}_{2}=\frac{4L}{{v}_{0}}$
故粒子从E点到F点所用的时间:t=t1+t2=$\frac{2\sqrt{3}πr+12L}{3{v}_{0}}$
答:(1)棒下落h的整个过程中,电阻上产生的电热是$\frac{BLmh}{2qR}{v}_{0}^{2}$-$\frac{{m}^{3}{v}_{0}^{6}}{16gBLR{q}^{3}}$.
(2)粒子从E点到F点所用的时间是$\frac{2\sqrt{3}πr+12L}{3{v}_{0}}$.
点评 本题是粒子在磁场中匀速圆周运动和电磁感应的综合.磁场中圆周运动常用方法是画轨迹,由几何知识求半径.

 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案 如图所示的电路中,理想变压器原、副线圈的匝数比n1:n2=22:5,原线圈接u1=220$\sqrt{2}$sin100πt(V)的交流电,电阻R1=R2=25Ω,D为理想二极管,则下列说法不正确的是( )
如图所示的电路中,理想变压器原、副线圈的匝数比n1:n2=22:5,原线圈接u1=220$\sqrt{2}$sin100πt(V)的交流电,电阻R1=R2=25Ω,D为理想二极管,则下列说法不正确的是( )| A. | 电阻R1两端的电压为50V | B. | 二极管的反向耐压值应大于50$\sqrt{2}$V | ||
| C. | 原线圈的输入功率为200W | D. | 通过R2的电流为$\sqrt{2}$A |
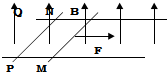 如图所示,两条足够长的光滑平行金属导轨水平放置导轨上,静止地放置两根质量相同、电阻相同的导体棒MN和PQ,两导体棒平行且垂直导轨,整个空间存在垂直于导轨平面的匀强磁场,不计导轨电阻,现在导体棒MN上施加一恒定的水平外力F,沿导轨向右运动,则下列说法正确的是( )
如图所示,两条足够长的光滑平行金属导轨水平放置导轨上,静止地放置两根质量相同、电阻相同的导体棒MN和PQ,两导体棒平行且垂直导轨,整个空间存在垂直于导轨平面的匀强磁场,不计导轨电阻,现在导体棒MN上施加一恒定的水平外力F,沿导轨向右运动,则下列说法正确的是( )| A. | 最终两导体棒都做匀速直线运动 | |
| B. | 最终两导体棒都做匀加速直线运动 | |
| C. | 导体棒MN上的电流一直增大 | |
| D. | 导体棒PQ上的电流先不断增大后保持不变 |
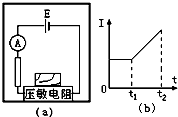 压敏电阻的阻值随着所受压力的增大而减小,在升降机中将重物放在压敏电阻上,压敏电阻接在如图(a)所示的电路中,电流表的示数变化情况如图(b)所示.某同学根据电流表的示数变化情况推断升降机的运动情况.下列推断正确的是( )
压敏电阻的阻值随着所受压力的增大而减小,在升降机中将重物放在压敏电阻上,压敏电阻接在如图(a)所示的电路中,电流表的示数变化情况如图(b)所示.某同学根据电流表的示数变化情况推断升降机的运动情况.下列推断正确的是( )| A. | 0-t1时间内,升降机一定匀速运动 | |
| B. | 0-t1时间内,升降机可能减速上升 | |
| C. | t1-t2时间内,升降机可能匀速上升 | |
| D. | t1-t2时间内,升降机可能匀加速上升 |
| A. | 核反应堆内发生的是轻核聚变反应 | |
| B. | 核反应堆内发生的是重核裂变反应 | |
| C. | 放射性同位素的半衰期由原子核内部因素决定,与外部条件及其变化无关 | |
| D. | 放射性同位素的半衰期既与原子核内部因素有关,也与外部条件有关 | |
| E. | 核反应过程中释放的γ射线是波长很短的电磁波,它具有很强的穿透本领 |
| A. | 扩散现象只发生在液体和气体中 | |
| B. | 从微观角度看气体的压强大小由分子的平均动能决定 | |
| C. | 在一定温度下,某种液体的饱和汽压是一定的 | |
| D. | 某种气体在温度升高的过程中对外放出热量是可能的 |
| A. |  原子中的电子绕原子核高速运转时,运行轨道的半径是任意的 | |
| B. | 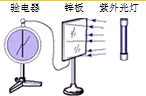 光电效应实验说明了光具有粒子性 | |
| C. |  电子束通过铝箔时的衍射图样证实了电子具有波动性 | |
| D. | 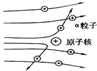 原子核式结构模型很好地解释了大角度散射实验现象 |
 如图所示,汽车在进行撞击实验时,安全气囊内迅速产生大量氮气而打开,气囊表面的气孔开始排气,若气囊表面有n个面积均为S的气孔,密度为ρ的氮气以速度v从气孔排出,氮气的摩尔质量为M,阿伏加德罗常数为NA,则在短时间t内排除的氮气分子数为$\frac{nSvtρ{N}_{A}}{M}$,设气囊内氮气不与外界进行热交换,则排气过程中气囊内温度降低(选填“升高”“不变”或“降低”)
如图所示,汽车在进行撞击实验时,安全气囊内迅速产生大量氮气而打开,气囊表面的气孔开始排气,若气囊表面有n个面积均为S的气孔,密度为ρ的氮气以速度v从气孔排出,氮气的摩尔质量为M,阿伏加德罗常数为NA,则在短时间t内排除的氮气分子数为$\frac{nSvtρ{N}_{A}}{M}$,设气囊内氮气不与外界进行热交换,则排气过程中气囊内温度降低(选填“升高”“不变”或“降低”)