题目内容
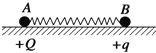
【题目】如图1所示，真空中相距d=5cm的两块平行金属板A、B与电源连接（图中未画出），其中B板接地（电势为零）。A板电势变化的规律如图2所示。将一个质量m=2.0×10－27kg，电量q=＋1.6×10－19C的带电粒子从紧临B板处释放，不计重力。求：
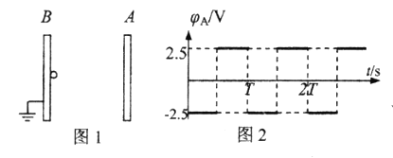
(1)在t=0时刻释放该带电粒子，释放瞬间粒子加速度的大小；
(2)若A板电势变化周期T=1.0×10－5s，在t=0时将带电粒子从紧临B板处无初速释放，粒子到达A板时速度的大小；
(3)A板电势变化周期多大时，在t=T/4时刻从紧临B板处无初速释放该带电粒子，粒子恰能到达A板。
【答案】（1）
（2）
（3）
【解析】
由图可知两板间开始时的电势差，则由
可求得两板间的电场强度，则可求得电场力，由牛顿第二定律可求得加速度的大小；因粒子受力可能发生变化，故由位移公式可求得粒子通过的距离，通过比较可知恰好到A板，故电场力不变，由动量定理可求得速度；要使粒子恰能到达A板，应让粒子在向A板运动中的总位移等于极板间的距离，由以上表达式可得出周期；
（1）电场强度
，带电粒子所受电场力
,
解得
；
（2）粒子在
时间内走过的距离为
故带电粒子在
时，恰好到达A板，
根据动量定理，此时粒子动量
，
又
，解得
；
（3）带电粒子在
向A板做匀加速运动，在
向A板做匀减速运动，速度减为零后将返回．粒子向A板运动可能的最大位移
要求粒子恰能到达A板，有
，可得
．
练习册系列答案
阅读快车系列答案
相关题目
