题目内容
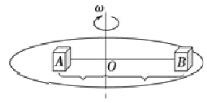
【题目】如图所示,固定的半球面右侧是光滑的,左侧是粗糙的,O点为球心,A、B为两个完全相同的小物块(可视为质点),小物块A静止在球面的左侧,受到的摩擦力大小为F1,对球面的压力大小为N1;小物块B在水平力F2作用下静止在球面的右侧,对球面的压力大小为N2,已知两小物块与球心连线和竖直方向的夹角均为θ,则 ( )

A. F1∶F2=cos2θ∶1
B. F1∶F2=sin2θ∶1
C. N1∶N2=cos2θ∶1
D. N1∶N2=sin2θ∶1
【答案】C
【解析】
分别对A、B两个相同的小物块受力分析,由受力平衡,求得所受的弹力,再根据牛顿第三定律,可得A、B分别对球面的压力大小之比。
对物体A,受重力、支持力和摩擦力,如下图所示,将物块A的重力沿半径和切面方向分解,可得:![]() ,
,![]() ,由牛顿第三定律可知:
,由牛顿第三定律可知:![]() ;
;
对物体B,受推力、重力和支持力,如下图所示,将物块B的重力和F2分别沿半径方向和切面方向分解,由平衡条件可得:![]() ,
,![]() ,
,
解得:![]() ,
,![]() ,由牛顿第三定律可知:
,由牛顿第三定律可知:![]() ;
;
故有:![]() ,
,![]() ,故选项C正确,ABD错误。
,故选项C正确,ABD错误。

练习册系列答案
相关题目