题目内容
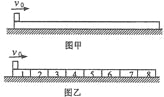
【题目】如图甲所示，一块长度为L=4m、质量为M=4kg的长木板静止放置在粗糙水平地面上。另有一质量为m=0.4kg的小铅块（可看做质点），以v0=5.5m/s的水平初速度向右冲上木板。已知铅块与木板间的动摩擦因数为
，木板与地面间的动摩擦因数为
，重力加速度取
.
（1）求铅块最终停在木板上的位置离木板最右端的距离d1（结果用分数表示）；
（2）若将木板平均分割长相同的八个木块，如图乙所示，其它条件不变：
①求木块开始运动瞬间，铅块的速度大小v1以及此时木块的加速度大小a1；
②确定铅块最终停在哪一块木块上并求出其停在该木块上的位置离该木块最右端的距离d2（计算结果用分数表示）。
【答案】（1）
（2）①
，
②停在第8块上，
【解析】
试题（1）因
，故木板一直对地静止
对铅块由动能定理：
可得：
（2）①因
，铅块滑上第7块前，所有木块对地静止，滑上第7块瞬间，第7/8块开始运动.
对铅块：
，得
，方向向左
对7、8块木块：
，得，方向向右
铅块冲上第7块瞬间速度为
:
，得
②设滑上第8块瞬间速度为
，则在第7块上的相对运动，以第7块作为参考系：
对第8块木板：
，得
，方向向右
则在第8块上的相对运动，以第8块作为参考系：
得：
练习册系列答案
相关题目
