题目内容
15.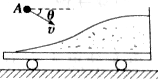 如图所示,一辆砂车的总质量为M,静止于光滑的水平面上,一个质量为m的物体A以速度v落入砂车中,v与水平方向成θ角,求物体落入砂车后车的速度v′.
如图所示,一辆砂车的总质量为M,静止于光滑的水平面上,一个质量为m的物体A以速度v落入砂车中,v与水平方向成θ角,求物体落入砂车后车的速度v′.
分析 以物体A与砂车为系统,水平方向动量守恒列出等式求解.
解答 解:以物体A与砂车为系统,水平方向动量守恒,选取向右为正方向,则:
mv•cosθ=(M+m)v′,
得球和砂车的共同速度
v′=$\frac{mvcosθ}{m+M}$.
答:物体落入砂车后车的速度是$\frac{mvcosθ}{m+M}$.
点评 解决该题关键掌握动量守恒的应用,正确选择研究对象是前提,系统所受合力不为零,但是可以在某一方向所受合力为零即在该方向上系统动量守恒.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
5. 空间某区域竖直平面内存在电场,电场线分布如图所示.一个质量为m、电量为q,电性未知的小球在该电场中运动,小球经过A点时的速度大小为v1,方向水平向右,运动至B点的速度大小为v2.若A、B两点之间的高度差为h,则以下判断中正确的是( )
空间某区域竖直平面内存在电场,电场线分布如图所示.一个质量为m、电量为q,电性未知的小球在该电场中运动,小球经过A点时的速度大小为v1,方向水平向右,运动至B点的速度大小为v2.若A、B两点之间的高度差为h,则以下判断中正确的是( )
 空间某区域竖直平面内存在电场,电场线分布如图所示.一个质量为m、电量为q,电性未知的小球在该电场中运动,小球经过A点时的速度大小为v1,方向水平向右,运动至B点的速度大小为v2.若A、B两点之间的高度差为h,则以下判断中正确的是( )
空间某区域竖直平面内存在电场,电场线分布如图所示.一个质量为m、电量为q,电性未知的小球在该电场中运动,小球经过A点时的速度大小为v1,方向水平向右,运动至B点的速度大小为v2.若A、B两点之间的高度差为h,则以下判断中正确的是( )| A. | A、B两点的电场强度和电势大小关系为EA<EB、φA<φB | |
| B. | 若v2>v1,则电场力一定做正功 | |
| C. | 若小球带正电,则A、B两点间的电势差为$\frac{m}{2q}$(v22-v12-2gh) | |
| D. | 小球从A运动到B点的过程中电场力做的功为$\frac{1}{2}$mv22-$\frac{1}{2}$mv12 |
6.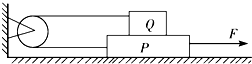 如图所示,位于水平桌面上的物块P,由跨过定滑轮的轻绳与物块相连,从滑轮到P和到Q的两段绳都是水平的,已知Q与P之间以及桌面之间的动摩擦因数都是μ,两物块的质量都是m,滑轮轴上的摩擦不计,若用一水平向右的力F拉P使其做匀速运动,则F的大小为( )
如图所示,位于水平桌面上的物块P,由跨过定滑轮的轻绳与物块相连,从滑轮到P和到Q的两段绳都是水平的,已知Q与P之间以及桌面之间的动摩擦因数都是μ,两物块的质量都是m,滑轮轴上的摩擦不计,若用一水平向右的力F拉P使其做匀速运动,则F的大小为( )
 如图所示,位于水平桌面上的物块P,由跨过定滑轮的轻绳与物块相连,从滑轮到P和到Q的两段绳都是水平的,已知Q与P之间以及桌面之间的动摩擦因数都是μ,两物块的质量都是m,滑轮轴上的摩擦不计,若用一水平向右的力F拉P使其做匀速运动,则F的大小为( )
如图所示,位于水平桌面上的物块P,由跨过定滑轮的轻绳与物块相连,从滑轮到P和到Q的两段绳都是水平的,已知Q与P之间以及桌面之间的动摩擦因数都是μ,两物块的质量都是m,滑轮轴上的摩擦不计,若用一水平向右的力F拉P使其做匀速运动,则F的大小为( )| A. | μmg | B. | 2μmg | C. | 3μmg | D. | 4μmg |
20. 如图所示,M、N两点有两等量异种点电荷,a、b、c表示电场中的3条等势线,b是M、N连线的中垂线,a、c关于b对称.点d、e、f、g是以O为圆心的圆与a、c的交点.已知一带负电的试探电荷从d点移动到e点时,该电荷的电势能增加.以下判断正确的是( )
如图所示,M、N两点有两等量异种点电荷,a、b、c表示电场中的3条等势线,b是M、N连线的中垂线,a、c关于b对称.点d、e、f、g是以O为圆心的圆与a、c的交点.已知一带负电的试探电荷从d点移动到e点时,该电荷的电势能增加.以下判断正确的是( )
 如图所示,M、N两点有两等量异种点电荷,a、b、c表示电场中的3条等势线,b是M、N连线的中垂线,a、c关于b对称.点d、e、f、g是以O为圆心的圆与a、c的交点.已知一带负电的试探电荷从d点移动到e点时,该电荷的电势能增加.以下判断正确的是( )
如图所示,M、N两点有两等量异种点电荷,a、b、c表示电场中的3条等势线,b是M、N连线的中垂线,a、c关于b对称.点d、e、f、g是以O为圆心的圆与a、c的交点.已知一带负电的试探电荷从d点移动到e点时,该电荷的电势能增加.以下判断正确的是( )| A. | M点处放置的是正电荷 | |
| B. | d点的电势高于f点的电势 | |
| C. | d点的场强与f点的场强相同 | |
| D. | 将带正电的试探电荷沿直线由d点移动到f点,电势能先增大后减小 |
5.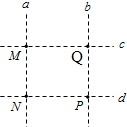 如图,直线a、b和c、d是处于匀强电场中的两组平行线,M、N、P、Q是它们的交点,四点处的电势分别为φM,φN,φP,φQ,一电子由M点分别到N点和P点的过程中,电场力所做的负功相等,则( )
如图,直线a、b和c、d是处于匀强电场中的两组平行线,M、N、P、Q是它们的交点,四点处的电势分别为φM,φN,φP,φQ,一电子由M点分别到N点和P点的过程中,电场力所做的负功相等,则( )
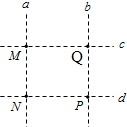 如图,直线a、b和c、d是处于匀强电场中的两组平行线,M、N、P、Q是它们的交点,四点处的电势分别为φM,φN,φP,φQ,一电子由M点分别到N点和P点的过程中,电场力所做的负功相等,则( )
如图,直线a、b和c、d是处于匀强电场中的两组平行线,M、N、P、Q是它们的交点,四点处的电势分别为φM,φN,φP,φQ,一电子由M点分别到N点和P点的过程中,电场力所做的负功相等,则( )| A. | 直线a位于某一等势面内,φM>φQ | |
| B. | 直线c位于某一等势面内,φM>φN | |
| C. | 若电子由M点运动到Q点,电场力做正功 | |
| D. | 若电子由P点运动到Q点,电场力做负功 |
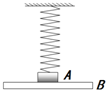 轻质弹簧上端固定,下端连接质量m=3kg的物块A,物块A放在平台B上,通过平台B可以控制A的运动,如图所示.初始时A、B静止,弹簧处于原长.已知弹簧的劲度系数k=200N/m,g=10m/s2.(计算结果保留两位有效数字)
轻质弹簧上端固定,下端连接质量m=3kg的物块A,物块A放在平台B上,通过平台B可以控制A的运动,如图所示.初始时A、B静止,弹簧处于原长.已知弹簧的劲度系数k=200N/m,g=10m/s2.(计算结果保留两位有效数字) 如图所示,在竖直平面内有一个粗糙的$\frac{1}{4}$圆弧轨道,其半径R=0.4m,轨道的最低点距地面高度h=0.8m,一质量m=0.1kg的小滑块从轨道的最高点A由静止释放,到达最低点B时的速度大小为v=2.0m/s.不计空气阻力,g取10m/s2,求:
如图所示,在竖直平面内有一个粗糙的$\frac{1}{4}$圆弧轨道,其半径R=0.4m,轨道的最低点距地面高度h=0.8m,一质量m=0.1kg的小滑块从轨道的最高点A由静止释放,到达最低点B时的速度大小为v=2.0m/s.不计空气阻力,g取10m/s2,求: