题目内容
如图所示，间距为L的光滑M、N金属轨道水平平行放置，ab是电阻为R0的金属棒，可紧贴导轨滑动，导轨右侧连接水平放置的平行板电容器，板间距为d，板长也为L，导轨左侧接阻值为R的定值电阻，其它电阻忽略不计．轨道处的磁场方向垂直轨道平面向下，电容器处的磁场垂直纸面向里，磁感应强度均为B．当ab以速度v0向右匀速运动时，一带电量大小为q的颗粒以某一速度从紧贴A板左侧平行于A板进入电容器内，恰好做匀速圆周运动，并刚好从C板右侧边缘离开．求：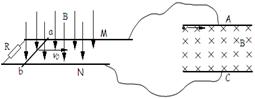
（1）AC两板间的电压U；
（2）带电颗粒的质量m；
（3）带电颗粒的速度大小v．
（1）
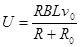（2）
（3）
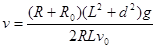
解析试题分析：（1）由法拉第电磁磁感应定律，ab棒的电动势为：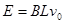
（2分）
设AC间的电压为U，由闭合电路欧姆定律，得：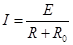
（2分），又U=IR（2分）
解得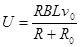：（2分）
（2）带电颗粒做匀速圆周运动，则重力与电场力平衡有：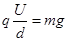
（2分）
解得： （2分）
（3）颗粒做匀速圆周运动，由牛顿第二定律可得：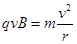
（2分）
颗粒运动轨迹如图所示，由几何关系可得：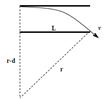
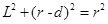（2分）
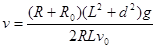解得： （2分）
考点：法拉第电磁磁感应定律，带电粒子在复合场中的运动，牛顿第二定律
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
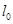的轻弹簧和一根长度为a的轻绳连接，弹簧的上端固定在天花板的O点上，P是位于O点正下方的光滑轻小定滑轮，已知
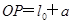.现将绳的另一端与静止在动摩擦因数恒定的水平地面上的滑块A相连，滑块对地面有压力作用．再用一水平力F作用于A使之向右做直线运动(弹簧的下端始终在P之上)，对于滑块A受地面滑动摩擦力下列说法中正确的是( )
=_________,如果地面的动摩擦因数变小，两者一起沿水平地面作匀加速运动，则
=
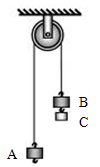
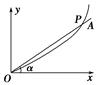
，绳长l=2m，绳的悬挂点O距水面的高度为H=3m。不考虑空气阻力和绳的质量，浮台露出水面的高度不计，水足够深。（取重力加速度
，
，
）
，平均阻力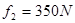
，求选手落入水中的深度
。
，为使小车恰好能通过圆形轨道的最高点D，则它在P点沿斜面向下的初速度v0。