题目内容
如图所示是游乐园内某种过山车的示意图。半径为R=8.0m的光滑圆形轨道固定在倾角θ=37°的斜轨道面上的A点,圆轨道的最高点D与车(视为质点)的初始位置P点平齐,B为圆轨道的最低点,C点与圆心O等高,圆轨道与斜轨道PA之间平滑连接。已知g=10 m/s2,sin37°=0.6,cos37°=0.8,车的质量m=100kg。求:
(1)若车从P点由静止开始下滑,恰能到达C点,则它经过B点时受圆轨道的支持力NB;
(2)若斜轨道面与小车间的动摩擦因数为 ,为使小车恰好能通过圆形轨道的最高点D,则它在P点沿斜面向下的初速度v0。
,为使小车恰好能通过圆形轨道的最高点D,则它在P点沿斜面向下的初速度v0。
(1)NB=3000N(2)v0=12 m/s
解析试题分析:(1)设小车经过B点时的速度为vB,从B到C的过程机械能守恒: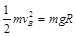 ………………①
………………①
小车在B点,由牛顿第二定律: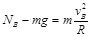 ………………②
………………②
联解①②代入数据得:
NB=3000N ………………③
(2)设P、A两点间距离为L,由几何关系可得: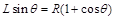 ………………④
………………④
设小车恰好通过圆形轨道时在D点的临界速度为vD,则: ………………⑤
………………⑤
小车从P运动到D,根据动能定理: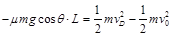 …………⑥
…………⑥
联解④⑤⑥得:
v0=12 m/s ………………⑦
考点:考查了机械能守恒,牛顿第二定律,动能定理,圆周运动

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
质量不同而具有相同动能的两个物体,在动摩擦因数相同的水平面上滑行到停止,则( )
| A.质量大的滑行的距离大 | B.质量大的滑行的时间长 |
| C.质量大的滑行的加速度小 | D.它们克服阻力做的功一样多 |
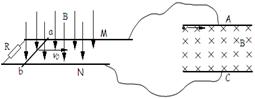
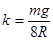 的弹性轻绳穿过圆环且固定在A、B两点。已知弹性轻绳满足胡克定律,形变量相同时弹性势能也相等,且弹性绳始终在弹性限度内,重力加速度为g,不计一切摩擦。将圆环由A点正下方的C点静止释放,当圆环运动到导轨的最低点D点时,求
的弹性轻绳穿过圆环且固定在A、B两点。已知弹性轻绳满足胡克定律,形变量相同时弹性势能也相等,且弹性绳始终在弹性限度内,重力加速度为g,不计一切摩擦。将圆环由A点正下方的C点静止释放,当圆环运动到导轨的最低点D点时,求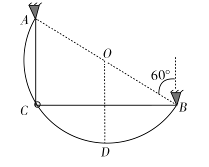

 ,电场宽度均为d,水平面粗糙摩擦系数为μ,一个质量为m,带正电的、电荷量为q的物体(看作质点),从第一个向右的电场区域的边缘由静止进入电场,则物体从开始运动到离开第2n个电场区域的过程中,求:
,电场宽度均为d,水平面粗糙摩擦系数为μ,一个质量为m,带正电的、电荷量为q的物体(看作质点),从第一个向右的电场区域的边缘由静止进入电场,则物体从开始运动到离开第2n个电场区域的过程中,求:

 圆弧形光滑轨道,半径R=
圆弧形光滑轨道,半径R= m,轨道端点B的切线水平。质量M="5" kg的金属滑块(可视为质点)由轨道顶端A由静止释放,离开B点后经时间t="1" s撞击在斜面上的P点。已知斜面的倾角
m,轨道端点B的切线水平。质量M="5" kg的金属滑块(可视为质点)由轨道顶端A由静止释放,离开B点后经时间t="1" s撞击在斜面上的P点。已知斜面的倾角 =37o,斜面底端C与B点的水平距离x0="3" m。g取10 m/s2,sin37o =0.6,cos37o =0.8,不计空气阻力。
=37o,斜面底端C与B点的水平距离x0="3" m。g取10 m/s2,sin37o =0.6,cos37o =0.8,不计空气阻力。
 0.25,求拉力F大小
0.25,求拉力F大小