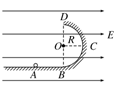
题目内容
一汽车重4 t，途经一圆弧形拱桥，圆弧半径为20 m.若桥最高处能承受的最大压力为2.94×104 N，则汽车速度多大时才能安全开过桥顶？
（g取9.8N/kg）提示:汽车过桥时不能压坏桥面也不能离开桥面.
（g取9.8N/kg）提示:汽车过桥时不能压坏桥面也不能离开桥面.
7m/s＜=" v" ＜ 14 m/s
本题考查圆周运动规律的应用，汽车途经一圆弧形拱桥做部分圆周运动，向心力由重力与支持力的合力提供，最高点桥能承受的压力等于零时，向心力最大，速度最大；最高点桥承受的压力最大时，向心力最小，速度最小.按此思路结合牛顿第二定律以及圆周运动知识分析求解即可.
汽车以速度v开过圆弧形拱桥顶，受重力mg和桥的支持力FN，其合力提供向心力Mg-FN=m分
，当桥最高处承受最大压力为FN′=2.94×104 N时，桥对汽车的最大支持力FN=FN′=2.94×104 N（依据牛顿第三定律），将FN代入上式，可求得汽车安全过桥的最小速度为
v1=
m/s="7" m/s
当FN=0（桥面不受力）时，有mg=m
，求得汽车安全过桥的最大速度为v2=
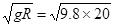m/s="14" m/s（当v＞
时，汽车将飞离桥顶，那是不安全的）.故当7 m/s≤v≤14 m/s时，汽车可安全开过桥顶.
汽车以速度v开过圆弧形拱桥顶，受重力mg和桥的支持力FN，其合力提供向心力Mg-FN=m分
，当桥最高处承受最大压力为FN′=2.94×104 N时，桥对汽车的最大支持力FN=FN′=2.94×104 N（依据牛顿第三定律），将FN代入上式，可求得汽车安全过桥的最小速度为v1=
m/s="7" m/s当FN=0（桥面不受力）时，有mg=m
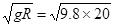，求得汽车安全过桥的最大速度为v2= m/s="14" m/s（当v＞时，汽车将飞离桥顶，那是不安全的）.故当7 m/s≤v≤14 m/s时，汽车可安全开过桥顶.
练习册系列答案
相关题目
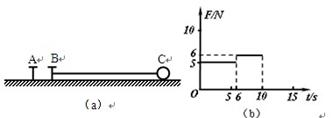
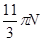
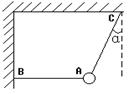
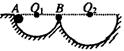
部分是半径为R的半圆形轨道，轨道的水平部分与其半圆相切，A为水平轨道上的一点，而且AB＝R＝0.2 m，把一质量m＝0.1 kg、带电荷量q＝＋1×10－4 C的小球放在水平轨道的A点由静止开始释放，小球在轨道的内侧运动．(g取10 m/s2)求： 