题目内容
18.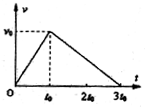 一质量为m的物体在水平恒定拉力F的作用下沿水平面运动,在t0时刻撤去F,其中v-t图象如图所示.已知物体与水平面间的动摩擦因数为μ,则下列说法正确的是( )
一质量为m的物体在水平恒定拉力F的作用下沿水平面运动,在t0时刻撤去F,其中v-t图象如图所示.已知物体与水平面间的动摩擦因数为μ,则下列说法正确的是( )①恒力F做功大小为2μmgv0t0
②0~2t0时间内物体克服摩擦力做功为$\frac{5}{4}$μmgv0t0
③$\frac{2}{3}$t0时刻恒力F功率大小为$\frac{4}{3}$μmgv0
④0~2t0时间内恒力F功率大小为$\frac{3}{4}$μmgv0.
| A. | ①③ | B. | ②④ | C. | ①②③ | D. | ②③④ |
分析 在v-t图象中,面积表示位移大小,据此求解各个时间段的位移大小;对全程根据动能定理列式求解拉力F,根据P=$\frac{W}{t}$求解平均功率,根据P=Fv求解瞬时功率.
解答 解:①取初速度方向为正方向,根据动量定理,对全过程:Ft0-μmg•3t0=0,
解得:F=3μmg;
0~t0时间内,位移为:x=$\frac{1}{2}{v}_{0}{t}_{0}$
故拉力的功为:W=Fx=3μmg•$\frac{1}{2}{v}_{0}{t}_{0}$=$\frac{3}{2}μmg{v}_{0}{t}_{0}$,故错误;
②0~2t0时间内,位移为:$x′=\frac{1}{2}{v}_{0}{t}_{0}+\frac{{v}_{0}+\frac{{v}_{0}}{2}}{2}{t}_{0}=\frac{5}{4}{v}_{0}{t}_{0}$
故0~2t0时间内物体克服摩擦力做功为:W=fx′=$\frac{5}{4}$μmgv0t0;故正确;
③$\frac{2}{3}$t0时刻的速度为$\frac{2}{3}{v}_{0}$,故$\frac{2}{3}$t0时刻恒力F功率大小为:P=Fv=3μmg•$\frac{2}{3}{v}_{0}$=2μmgv0,故错误;
④0~2t0时间内,只有前一半时间做功,为:W=Fx=$\frac{3}{2}μmg{v}_{0}{t}_{0}$;故在0~2t0时间内拉力的平均功率为:
P=$\frac{W}{t}=\frac{\frac{3}{2}μmg{v}_{0}{t}_{0}}{2{t}_{0}}=\frac{3}{4}μmg{v}_{0}$,故正确;
故选:B
点评 本题涉及力在时间上的累积效应,可优先考虑运用动量定理研究F的大小,当然也可以根据牛顿第二定律和运动学公式结合求解.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案 我国正在进行的探月工程是高新技术领域的一次重大科技活动,在探月工程中飞行器成功变轨至关重要.如图所示,假设月球半径为R,月球表面的重力加速度为g0,飞行器在距月球表面高度为3R的圆形轨道Ⅰ运动,到达轨道的A点点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B再次点火进入近月轨道Ⅲ绕月球做圆周运动.则( )
我国正在进行的探月工程是高新技术领域的一次重大科技活动,在探月工程中飞行器成功变轨至关重要.如图所示,假设月球半径为R,月球表面的重力加速度为g0,飞行器在距月球表面高度为3R的圆形轨道Ⅰ运动,到达轨道的A点点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B再次点火进入近月轨道Ⅲ绕月球做圆周运动.则( )| A. | 飞行器在B点处点火后,动能增加 | |
| B. | 由已知条件不能求出飞行器在Ⅱ轨道上运行周期 | |
| C. | 只有万有引力作用下,飞行器在轨道Ⅱ上通过B点的加速度大于在轨道Ⅲ在B点的加速度 | |
| D. | 飞行器在轨道Ⅲ绕月球运行一周所需的时间为2π$\sqrt{\frac{R}{{g}_{0}}}$ |
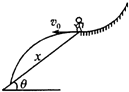 在某次自由式滑雪比赛中,运动员在较高的雪坡上滑到某一弧形部位处,沿水平方向飞出,在空中划过一段抛物线后,再落到雪坡上,如图所示,若忽略空气阻力,雪坡的倾角为θ,飞出时的速度大小为v0,则下列说法错误的是( )
在某次自由式滑雪比赛中,运动员在较高的雪坡上滑到某一弧形部位处,沿水平方向飞出,在空中划过一段抛物线后,再落到雪坡上,如图所示,若忽略空气阻力,雪坡的倾角为θ,飞出时的速度大小为v0,则下列说法错误的是( )| A. | 运动员在空中经历的时间是$\frac{2{v}_{0}tanθ}{g}$ | |
| B. | 运动员的落点与起飞点的距离是$\frac{2{{v}^{2}}_{0}sinθ}{gco{s}^{2}θ}$ | |
| C. | 运动员落回斜坡时的速度大小是$\frac{{v}_{0}}{cosθ}$ | |
| D. | 运动员的落点与起飞点间竖直高度是$\frac{2{{v}^{2}}_{0}ta{n}^{2}θ}{g}$ |
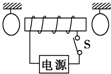 如图所示,通电螺线管两侧各悬挂一个小铜环,铜环平面与螺线管截面平行.当电键S接通瞬间,关于两铜环的运动情况下列说法错误的是( )
如图所示,通电螺线管两侧各悬挂一个小铜环,铜环平面与螺线管截面平行.当电键S接通瞬间,关于两铜环的运动情况下列说法错误的是( )| A. | 同时向两侧推开 | |
| B. | 同时向螺线管靠拢 | |
| C. | 一个被推开,一个被吸引,但因电源正负极未知,无法具体判断 | |
| D. | 同时被推开或同时向螺线管靠拢,因电源正负极未知,无法具体判断 |
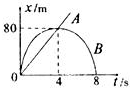 如图所示是A、B两质点从同一地点做直线运动的位移随时间变化的x-t图象,则下列说法中正确的是( )
如图所示是A、B两质点从同一地点做直线运动的位移随时间变化的x-t图象,则下列说法中正确的是( )| A. | A质点做匀加速直线运动 | |
| B. | A、B两质点在8s末相遇 | |
| C. | B质点最初4s做减速运动,后4s做加速运动 | |
| D. | B质点先沿负方向做直线运动,后沿正方向做直线运动 |
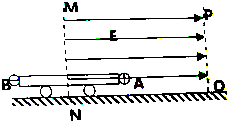 如图所示,长为2L的平板绝缘小车放在光滑水平面上,小车两端固定两个绝缘的带电小球A和B,A、B所带电荷量分别为+2q和-3q,小车(包括带电小球A、B)的总质量为m,虚线MN与PQ均沿竖直方向且相距3L,开始时虚线MN位于小车正中间,若视带电小球为质点,在虚线MN、PQ间加上方向水平向右、场强大小为E的匀强电场后,小车开始运动,
如图所示,长为2L的平板绝缘小车放在光滑水平面上,小车两端固定两个绝缘的带电小球A和B,A、B所带电荷量分别为+2q和-3q,小车(包括带电小球A、B)的总质量为m,虚线MN与PQ均沿竖直方向且相距3L,开始时虚线MN位于小车正中间,若视带电小球为质点,在虚线MN、PQ间加上方向水平向右、场强大小为E的匀强电场后,小车开始运动, 如图为一单摆的共振曲线,
如图为一单摆的共振曲线,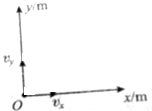 如图所示,质点在一平面内运动,在x方向质点做匀速直线运动,速度大小vx=3m/s,方向沿x轴正方向;在y方向质点也做匀速直线运动,速度大小vy=4m/s,方向沿y轴正方向,在t=0时,质点恰好在坐标原点O.
如图所示,质点在一平面内运动,在x方向质点做匀速直线运动,速度大小vx=3m/s,方向沿x轴正方向;在y方向质点也做匀速直线运动,速度大小vy=4m/s,方向沿y轴正方向,在t=0时,质点恰好在坐标原点O.