题目内容
8.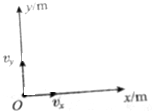 如图所示,质点在一平面内运动,在x方向质点做匀速直线运动,速度大小vx=3m/s,方向沿x轴正方向;在y方向质点也做匀速直线运动,速度大小vy=4m/s,方向沿y轴正方向,在t=0时,质点恰好在坐标原点O.
如图所示,质点在一平面内运动,在x方向质点做匀速直线运动,速度大小vx=3m/s,方向沿x轴正方向;在y方向质点也做匀速直线运动,速度大小vy=4m/s,方向沿y轴正方向,在t=0时,质点恰好在坐标原点O.(1)在t=1s时,求出质点的位置坐标,速度的大小和方向;
(2)在t=2s时,求出质点的位置坐标,速度的大小和方向;
(3)质点的运动轨迹第直线还是曲线?
分析 (1、2)质点在x方向上做匀速直线运动,y方向上做匀速直线运动,结合运动学公式求出质点的位置坐标.根据平行四边形定则求出质点的速度大小和方向.
(3)根据合速度的大小和方向确定运动的轨迹.
解答 解:(1)t=1s时,x方向上的位移x=vxt1=3×1m=3m,y方向上的位移y=vyt1=4×1m=4m,
质点的位移坐标为(3m,4m)
根据平行四边形定则知,质点的速度大小v=$\sqrt{{{v}_{x}}^{2}+{{v}_{y}}^{2}}=\sqrt{9+16}m/s=5m/s$.
根据tanα=$\frac{{v}_{y}}{{v}_{x}}=\frac{4}{3}$知,速度方向与x轴方向的夹角为53°.
(2)t=2s时,x方向上的位移x=vxt2=3×2m=6m,y方向上的位移y=vyt2=4×2m=8m,
质点的位移坐标为(6m,8m)
根据平行四边形定则知,质点的速度大小v=$\sqrt{{{v}_{x}}^{2}+{{v}_{y}}^{2}}=\sqrt{9+16}m/s=5m/s$.
根据tanα=$\frac{{v}_{y}}{{v}_{x}}=\frac{4}{3}$知,速度方向与x轴方向的夹角为53°.
(3)因为合速度是定值,方向不变,知质点的运动轨迹是直线.
答:(1)质点的位置坐标为(3m,4m),速度的大小为5m/s,方向与x轴方向的夹角为53°;
(2)质点的位置坐标为(6m,8m),速度的大小为5m/s,方向与x轴方向的夹角为53°;
(3)质点的运动轨迹是直线.
点评 本题考查了运动学的合成与分解,知道速度、位移都是时刻,合成和分解遵循平行四边形定则.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.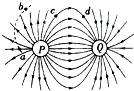 P、Q两电荷形成的电场的电场线分布如图所示,a、b、c、d为电场中的四个点.一个离子从a运动到b(不计重力),轨迹如图所示.则下列判断正确的是( )
P、Q两电荷形成的电场的电场线分布如图所示,a、b、c、d为电场中的四个点.一个离子从a运动到b(不计重力),轨迹如图所示.则下列判断正确的是( )
 P、Q两电荷形成的电场的电场线分布如图所示,a、b、c、d为电场中的四个点.一个离子从a运动到b(不计重力),轨迹如图所示.则下列判断正确的是( )
P、Q两电荷形成的电场的电场线分布如图所示,a、b、c、d为电场中的四个点.一个离子从a运动到b(不计重力),轨迹如图所示.则下列判断正确的是( )| A. | 离子带正电 | |
| B. | c点电势高于d点电势 | |
| C. | 离子在a点时加速度大于b点时加速度 | |
| D. | 离子在a点时电势能大于b点时电势能 |
3.下列说法正确的是( )
| A. | 有摩擦力的地方一定有弹力 | |
| B. | 运动的物体不会受到静摩擦力 | |
| C. | 织纱成布,是因为棉纱之间存在摩擦力 | |
| D. | 摩擦力的方向一定与物体运动方向在同一直线上 |
17.如图甲,手提电脑散热底座一般设置有四个卡位用来调节角度.某同学将电脑放在散热底座上,为了获得更好的舒适度,由原卡位1调至卡位4(如图乙),电脑始终处于静止状态,分析正确的是( ) 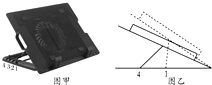

| A. | 电脑受到的支持力变小 | |
| B. | 电脑受到的摩擦力变大 | |
| C. | 散热底座对电脑作用力的合力不变 | |
| D. | 电脑受到的支持力与摩擦力的大小之和大于其重力 |
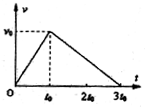 一质量为m的物体在水平恒定拉力F的作用下沿水平面运动,在t0时刻撤去F,其中v-t图象如图所示.已知物体与水平面间的动摩擦因数为μ,则下列说法正确的是( )
一质量为m的物体在水平恒定拉力F的作用下沿水平面运动,在t0时刻撤去F,其中v-t图象如图所示.已知物体与水平面间的动摩擦因数为μ,则下列说法正确的是( )
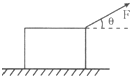 如图所示,质量m=2kg的物体静止在水平地面上,物体与水平面间的滑动摩擦力大小等于它们间弹力的0.25倍,现对物体施加一个大小F=8N、与水平方向夹角θ=37°角的斜向上的拉力,已知sin37°=0.6,cos37°=0.8,g取10m/s2.求:
如图所示,质量m=2kg的物体静止在水平地面上,物体与水平面间的滑动摩擦力大小等于它们间弹力的0.25倍,现对物体施加一个大小F=8N、与水平方向夹角θ=37°角的斜向上的拉力,已知sin37°=0.6,cos37°=0.8,g取10m/s2.求: 面积为s的矩形线框abcd,处在磁感应强度为B的匀强磁场中(磁场区域足够大),磁场方向与线框平面成θ角,如图所示.
面积为s的矩形线框abcd,处在磁感应强度为B的匀强磁场中(磁场区域足够大),磁场方向与线框平面成θ角,如图所示.