题目内容
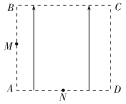
【题目】(18分)如图所示,光滑的水平导轨![]() 右端
右端![]() 处与水平传送带理想连接,传送带长度
处与水平传送带理想连接,传送带长度![]() = 4.0 m,皮带以恒定速率
= 4.0 m,皮带以恒定速率![]() = 3.0 m/s 顺时针转动.三个质量均为
= 3.0 m/s 顺时针转动.三个质量均为![]() = 1.0 kg 的滑块
= 1.0 kg 的滑块![]() 、
、![]() 、
、![]() 置于水平导轨上,
置于水平导轨上,![]() 、
、![]() 之间有一段轻弹簧刚好处于原长,滑块
之间有一段轻弹簧刚好处于原长,滑块![]() 与轻弹簧连接,
与轻弹簧连接,![]() 未连接弹簧,
未连接弹簧,![]() 、
、![]() 处于静止状态且离
处于静止状态且离![]() 点足够远,现让滑块
点足够远,现让滑块![]() 以初速度
以初速度![]() = 3.0 m/s 沿
= 3.0 m/s 沿![]() 、
、![]() 连线方向向
连线方向向![]() 运动,
运动,![]() 与
与![]() 碰撞后粘合在一起,碰撞时间极短.滑块
碰撞后粘合在一起,碰撞时间极短.滑块![]() 脱离弹簧后滑上传送带,并从右端
脱离弹簧后滑上传送带,并从右端![]() 滑出落至地面上.已知滑块
滑出落至地面上.已知滑块![]() 与传送带之间的动摩擦因数
与传送带之间的动摩擦因数![]() = 0.1,重力加速度
= 0.1,重力加速度![]() =10m/s2.求:
=10m/s2.求:

(1)滑块![]() 、
、![]() 碰撞时损失的机械能;
碰撞时损失的机械能;
(2)滑块![]() 在传送带上因摩擦产生的热量
在传送带上因摩擦产生的热量![]() ;
;
(3)若每次实验开始时滑块![]() 的初速度
的初速度![]() 大小不相同,要使滑块
大小不相同,要使滑块![]() 滑上传送带后总能落至地面上的同一位置,则
滑上传送带后总能落至地面上的同一位置,则![]() 的取值范围是什么?
的取值范围是什么?
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]() m/s
m/s![]()
![]() m/s
m/s
【解析】
试题分析:(1)设A和B碰撞后共同速度为![]() ,对A、B有:
,对A、B有:
动量守恒 ![]() ①
①
碰撞时损失机械能![]() ②
②
解得![]() .
.
(2)设AB碰撞后,弹簧第一次恢复原长时AB的速度为![]() ,C的速度为
,C的速度为![]() 。对A、B、C和弹簧组成的系统从AB碰撞后到弹簧第一次恢复原长的过程中,有:
。对A、B、C和弹簧组成的系统从AB碰撞后到弹簧第一次恢复原长的过程中,有:
动量守恒:![]() ③
③
机械能守恒:![]() ④
④
解得:![]()
C以![]() 滑上传送带,假设匀加速直线运动位移为
滑上传送带,假设匀加速直线运动位移为![]() 时与传送带共速,由运动学公式
时与传送带共速,由运动学公式![]()
解得![]() m<
m<![]()
加速运动的时间为![]() ,有:
,有:![]() s ⑤
s ⑤
C在传送带上滑过的相对位移为![]() m ⑥
m ⑥
摩擦生热![]()
(3)设A的最大速度为![]() ,滑块C在与弹簧分离时
,滑块C在与弹簧分离时![]() 的速度为
的速度为![]() 、AB的速度为
、AB的速度为![]() ,则C在传送带上一直匀减速直线运动直到在P点与传送带共速,有:
,则C在传送带上一直匀减速直线运动直到在P点与传送带共速,有:
![]() ⑦
⑦
解得:![]() m/s
m/s
设A的最小速度为![]() ,滑块C在与弹簧分离时
,滑块C在与弹簧分离时![]() 的速度为
的速度为![]() 、AB的速度为
、AB的速度为![]() ,则C在传送带上一直匀加速直线运动直到在P点与传送带共速,有:
,则C在传送带上一直匀加速直线运动直到在P点与传送带共速,有:![]() ⑧ 解得
⑧ 解得![]() m/s
m/s
对A、B、C和弹簧组成的系统从AB碰撞后到弹簧第一次恢复原长的过程中,有:
动量守恒: ![]() ⑨
⑨
机械能守恒: ![]() ⑩
⑩
解得![]() m/s
m/s
同理![]()
![]() m/s
m/s
所以 ![]() m/s
m/s![]()
![]() m/s
m/s

 出彩同步大试卷系列答案
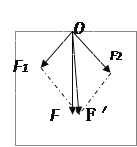
出彩同步大试卷系列答案【题目】(1)在“验证力的平行四边形定则”实验中,用两个弹簧测力计分别钩住细绳套,互成角度地拉橡皮条,使它伸长到某一位置O点,这一步操作中必须记录的是( )
A.橡皮条固定端得位置 |
B.描下O点的位置和两细绳的方向 |
C.橡皮条伸长后的总长度 |
D.两个弹簧测力计的读数 |
(2)做实验时,根据测量结果在白纸上画出如图所示的图示图中O为橡皮条与细绳套的结点,图中________是F1和F2的合力的理论值;________是F1和F2的合力的实际测量值