题目内容
19.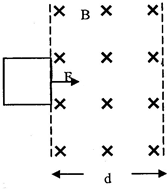 粗糙的水平面上有一个正方形线框,其边长为0.5m,质量为1.5kg,电阻为0.2Ω,线框与水平地面间的动摩擦因数μ=0.4.图中虚线区域内磁场的磁感应强度为0.4T.线框初始位置如图所示,受到拉力F作用后做初速为0,加速度为1m/s2的匀加速直线运动,等到线框左边刚进入磁场时,立即撤去F,结果线框右边滑到磁场的右边缘处速度刚好减为0,取g=10m/s2,则( )
粗糙的水平面上有一个正方形线框,其边长为0.5m,质量为1.5kg,电阻为0.2Ω,线框与水平地面间的动摩擦因数μ=0.4.图中虚线区域内磁场的磁感应强度为0.4T.线框初始位置如图所示,受到拉力F作用后做初速为0,加速度为1m/s2的匀加速直线运动,等到线框左边刚进入磁场时,立即撤去F,结果线框右边滑到磁场的右边缘处速度刚好减为0,取g=10m/s2,则( )| A. | 线框运动的总时间为1.25s | |
| B. | 磁场区域的宽度d为0.625m | |
| C. | 从开始至线圈速度减为0的过程中,通过线圈横截面的电荷量为0.5C | |
| D. | 在线圈进入磁场的过程中,作用力F与时间t的关系式为F=1.5+0.2t(N) |
分析 线框开始做初速度为零的匀加速直线运动,后做匀减速直线运动,应用匀变速直线运动的速度公式与位移公式可以求出线框的运动时间与磁场宽度;
由法拉第电磁感应定律求出感应电动势,由欧姆定律求出电流,然后由电流定义式求出电荷量;
应用安培力公式求出安培力,应用牛顿第二定律可以求出拉力.
解答 解:A、线框进入磁场过程做匀加速直线运动,位移等于线框的边长,v2=2aL,解得:v=$\sqrt{2aL}$=1m/s,线框进入磁场的时间:t1=$\frac{v}{a}$=$\frac{1}{1}$=1s,线框完全在磁场中的运动时间:t2=$\frac{v}{μg}$=$\frac{1}{0.4×10}$=0.25s,线框总的运动时间:t=t1+t2=1.25s,故A正确;
B、磁场的宽度等于线框的位移,磁场宽度:d=x1+x2=$\frac{v}{2}$t1+$\frac{v}{2}$t2=$\frac{v}{2}$t=$\frac{1}{2}$×1.25=0.625m,故B正确;
C、感应电动势:$\overline{E}$=$\frac{△Φ}{△t}$=$\frac{BS}{△t}$=$\frac{BLd}{△t}$,感应电流:I=$\frac{\overline{E}}{R}$,电荷量:q=I△t=$\frac{BLd}{R}$=$\frac{0.4×0.5×0.625}{0.2}$=0.625C,故C错误;
D、感应电动势:E=BLv=BLat,感应电流:I=$\frac{E}{R}$=$\frac{BLat}{R}$=$\frac{0.4×0.5×1×t}{0.2}$=tA,线框受到的安培力:F安培=BIL=0.4×t×0.5=0.2t,
对线框,由牛顿第二定律得:F-F安培-μmg=ma,解得:F=F安培+μmg+ma=(7.5+0.2t)N,故D错误;
故选:AB.
点评 本题是一道电磁感应、电路与运动学相结合的综合题,有一定难度,分析清楚线框的运动过程是正确解题的关键,应用匀变速运动规律、牛顿第二定律、法拉第电磁感应定律、欧姆定律与电流定义式可以解题;解题时要注意线框始终受到摩擦阻力的作用,这点是容易忽视的地方.

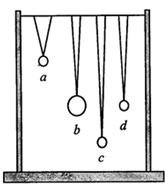 在一条张紧的绳子上挂着四个摆,其中b、d摆长相等.当b摆开始摆动后,其余三个也跟着摆动起来,达到稳定时( )
在一条张紧的绳子上挂着四个摆,其中b、d摆长相等.当b摆开始摆动后,其余三个也跟着摆动起来,达到稳定时( )| A. | d摆的振幅比a、c摆的振幅都要大 | |
| B. | 四个摆振动时的频率相同,振幅也相同 | |
| C. | c摆摆长最大,所以振动时c摆的振动周期最大 | |
| D. | a、c、d摆振动的周期相同,但比b摆要略小些 |
 在如图所示的电路中,已知电灯的阻值为10Ω,电阻R的阻值为100Ω,交流电源的电压U=220$\sqrt{2}$sin100πt(V),则( )
在如图所示的电路中,已知电灯的阻值为10Ω,电阻R的阻值为100Ω,交流电源的电压U=220$\sqrt{2}$sin100πt(V),则( )| A. | 电灯消耗的实际功率为80W | B. | 电阻R两端的电压为200$\sqrt{2}$V | ||
| C. | 电路中交变电流的频率为100Hz | D. | 电路中的电流方向每秒改变100次 |
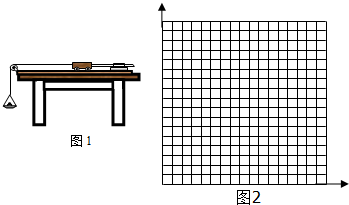
(1)上述处理必需满足的条件是M>>m,本实验中是否需要平衡摩擦力是(填“是”或“否”).
(2)他们利用图象探究功与速度的关系,你认力最合理的应该用下述哪种图象B.
A.W-v图象 B.W-v2图象 C.W-$\frac{1}{v}$图象 D.W-$\frac{1}{{v}^{2}}$图象
(3)你如何判断实验过程中小车是否从静止开始运动?图象W-v2是否是经过原点的倾斜的直线.或从第一个打点开始,小车通过的位移之比是否为1:3:5…
(4)上述实验中,该组得到了如表所示的实验数据,请根据数据在图2坐标纸上画出(2)中你选择的图象.
| 功W/J | 0.02 | 0.04 | 0.06 | 0.08 | 0.10 | 0.12 |
| 速度v/ms-1 | 0.13 | 0.20 | 0.24 | 0.25 | 0.33 | 0.35 |
 如图所示,质量分别为m1、m2的两个物块间用一轻弹簧连接,放在倾角为θ的光滑斜面上.平行于斜面、大小为F的拉力作用在m1上,使m1、m2一起向上作匀加速运动,斜面始终静止在水平地面上,则( )
如图所示,质量分别为m1、m2的两个物块间用一轻弹簧连接,放在倾角为θ的光滑斜面上.平行于斜面、大小为F的拉力作用在m1上,使m1、m2一起向上作匀加速运动,斜面始终静止在水平地面上,则( )| A. | 弹簧的弹力为$\frac{{m}_{2}}{{m}_{1}+{m}_{2}}$F | B. | 弹簧的弹力为$\frac{{m}_{1}}{{m}_{1}+{m}_{2}}$F | ||
| C. | 地面对斜面的摩擦力水平向左 | D. | 地面对斜面的摩擦力水平向右 |

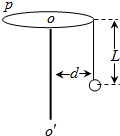 某游乐场中有一种叫“空中飞椅”的游乐设施,其基本装置是将绳子上端固定在转盘的边缘上,绳子下端连接座椅,人坐在座椅上随转盘旋转而在空中飞旋.若将人和座椅看成是一个可视为质点的小球,该物理情景可简化为如图所示的物理模型.其中P为处于水平面内的转盘,可绕竖直转轴OO′转动,设绳长L=10m,小球的质量 m=60kg,转盘静止时小球与转轴之间的距离d=4m.转盘逐渐加速转动,经过一段时间后小球与转盘一起做匀速圆周运动,此时绳子与竖直方向的夹角θ=37°(不计空气阻力、绳子的重力和绳子的形变量,已知sin37°=0.6,cos37°=0.8,g=10m/s2)求:
某游乐场中有一种叫“空中飞椅”的游乐设施,其基本装置是将绳子上端固定在转盘的边缘上,绳子下端连接座椅,人坐在座椅上随转盘旋转而在空中飞旋.若将人和座椅看成是一个可视为质点的小球,该物理情景可简化为如图所示的物理模型.其中P为处于水平面内的转盘,可绕竖直转轴OO′转动,设绳长L=10m,小球的质量 m=60kg,转盘静止时小球与转轴之间的距离d=4m.转盘逐渐加速转动,经过一段时间后小球与转盘一起做匀速圆周运动,此时绳子与竖直方向的夹角θ=37°(不计空气阻力、绳子的重力和绳子的形变量,已知sin37°=0.6,cos37°=0.8,g=10m/s2)求: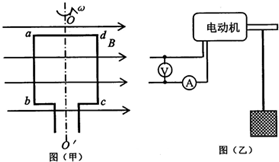 如图所示,一个矩形线圈abcd处于磁感应强度为B的匀强磁场中,并以OO′为轴做匀速圆周运动,(OO′与磁场方向垂直,线圈电阻为r),线圈转动的角速度为ω,用该线圈产生的交变电流通入电阻为R的电动机,电动机通过细绳把质量为m的重物从静止开始竖直向上拉起这一过程中,电压表示数为U,电流表示数为I.
如图所示,一个矩形线圈abcd处于磁感应强度为B的匀强磁场中,并以OO′为轴做匀速圆周运动,(OO′与磁场方向垂直,线圈电阻为r),线圈转动的角速度为ω,用该线圈产生的交变电流通入电阻为R的电动机,电动机通过细绳把质量为m的重物从静止开始竖直向上拉起这一过程中,电压表示数为U,电流表示数为I.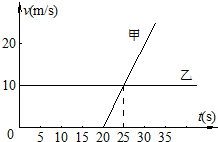 汽车甲和摩托车乙从同一地点沿同一方向运动,运动情况如图所示.则两车在t=40s时相遇,两车相遇前的最大距离为225m.
汽车甲和摩托车乙从同一地点沿同一方向运动,运动情况如图所示.则两车在t=40s时相遇,两车相遇前的最大距离为225m.