题目内容
9.如图所示,AB为固定在竖直平面内半径为R的四分之一光滑圆弧轨道,轨道在B点与光滑的水平面BC相切,质量为m的小球在A点静止释放,求:
(1)小球滑到最低点B时速度的大小;
(2)小球通过BC滑上固定曲面CD,恰好到达最高点D,D到水平面的高度为h,则小球在曲面CD上滑过程中克服摩擦力所做的功是多少.
分析 (1)小球沿AB圆弧下滑时,只有重力做功,机械能守恒,由机械能守恒定律求小球滑到最低点B时速度的大小.
(2)对于B到D过程,运用动能定理可求克服摩擦力所做的功.也可对AD过程,由动能定理求.
解答 解:(1)AB过程,由机械能守恒定律得
mgR=$\frac{1}{2}m{v}_{B}^{2}$
得 vB=$\sqrt{2gR}$
(2)设小球在曲面CD上滑过程中克服摩擦力所做的功是W.
对于A到D的过程,由动能定理得:
mg(R-h)-W=0
解得 W=mg(R-h)
答:
(1)小球滑到最低点B时速度的大小是$\sqrt{2gR}$;
(2)小球在曲面CD上滑过程中克服摩擦力所做的功是mg(R-h).
点评 本题要分析清楚物体的运动情况,正确选择研究过程,知道机械能守恒定律和动能定理的区别.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.如图为一列向右传播的横波在某时刻的波形图,则下列说法中正确的是 ( )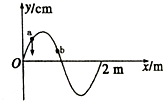

| A. | 质点b此时向右运动 | B. | 质点b此时向y轴正方向运动 | ||
| C. | 此时质点a比质点b的速度大 | D. | 质点a比质点b的振幅大 |
20. 如图所示,轻杆的一端有一个小球m,另一端有光滑的固定转轴O.现给小球一初速度v,使小球和杆一起绕O轴在竖直面内转动,不计空气阻力,用F表示小球到达最高点时杆对小球的作用力,则F( )
如图所示,轻杆的一端有一个小球m,另一端有光滑的固定转轴O.现给小球一初速度v,使小球和杆一起绕O轴在竖直面内转动,不计空气阻力,用F表示小球到达最高点时杆对小球的作用力,则F( )
 如图所示,轻杆的一端有一个小球m,另一端有光滑的固定转轴O.现给小球一初速度v,使小球和杆一起绕O轴在竖直面内转动,不计空气阻力,用F表示小球到达最高点时杆对小球的作用力,则F( )
如图所示,轻杆的一端有一个小球m,另一端有光滑的固定转轴O.现给小球一初速度v,使小球和杆一起绕O轴在竖直面内转动,不计空气阻力,用F表示小球到达最高点时杆对小球的作用力,则F( )| A. | 一定是拉力 | |
| B. | 一定是支持力 | |
| C. | 一定等于0 | |
| D. | 可能是拉力,可能是支持力,也可能等于0 |
17.质量为2kg的小铁球从某一高度由静止释放,经3s到达地面,不计空气阻力,下列说法正确的是( )
| A. | 3s内重力所做的功为900J | B. | 3s内重力所做的功为200J | ||
| C. | 3s末重力的瞬时功率为900W | D. | 3s内重力的平均功率为400W |
14.天文学家新发现了太阳系外的一颗行星.已知该行星的某一近地卫星绕行星圆周运动的周期约为1.4小时,引力常量G=6.67×10-11N•m2/kg2,由此估算该行星的平均密度为( )
| A. | 5.6×103kg/m3 | B. | 7.2×1010kg/m3 | C. | 2.8×107kg/m3 | D. | 1.0×107kg/m3 |
18.一物体受到几个共点的恒力作用而处于平衡状态,当撤去某个恒力后,物体不可能做( )
| A. | 匀加速直线运动 | B. | 匀减速直线运动 | C. | 匀变速曲线运动 | D. | 变加速曲线运动 |
19.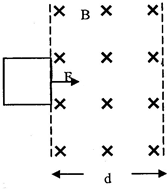 粗糙的水平面上有一个正方形线框,其边长为0.5m,质量为1.5kg,电阻为0.2Ω,线框与水平地面间的动摩擦因数μ=0.4.图中虚线区域内磁场的磁感应强度为0.4T.线框初始位置如图所示,受到拉力F作用后做初速为0,加速度为1m/s2的匀加速直线运动,等到线框左边刚进入磁场时,立即撤去F,结果线框右边滑到磁场的右边缘处速度刚好减为0,取g=10m/s2,则( )
粗糙的水平面上有一个正方形线框,其边长为0.5m,质量为1.5kg,电阻为0.2Ω,线框与水平地面间的动摩擦因数μ=0.4.图中虚线区域内磁场的磁感应强度为0.4T.线框初始位置如图所示,受到拉力F作用后做初速为0,加速度为1m/s2的匀加速直线运动,等到线框左边刚进入磁场时,立即撤去F,结果线框右边滑到磁场的右边缘处速度刚好减为0,取g=10m/s2,则( )
 粗糙的水平面上有一个正方形线框,其边长为0.5m,质量为1.5kg,电阻为0.2Ω,线框与水平地面间的动摩擦因数μ=0.4.图中虚线区域内磁场的磁感应强度为0.4T.线框初始位置如图所示,受到拉力F作用后做初速为0,加速度为1m/s2的匀加速直线运动,等到线框左边刚进入磁场时,立即撤去F,结果线框右边滑到磁场的右边缘处速度刚好减为0,取g=10m/s2,则( )
粗糙的水平面上有一个正方形线框,其边长为0.5m,质量为1.5kg,电阻为0.2Ω,线框与水平地面间的动摩擦因数μ=0.4.图中虚线区域内磁场的磁感应强度为0.4T.线框初始位置如图所示,受到拉力F作用后做初速为0,加速度为1m/s2的匀加速直线运动,等到线框左边刚进入磁场时,立即撤去F,结果线框右边滑到磁场的右边缘处速度刚好减为0,取g=10m/s2,则( )| A. | 线框运动的总时间为1.25s | |
| B. | 磁场区域的宽度d为0.625m | |
| C. | 从开始至线圈速度减为0的过程中,通过线圈横截面的电荷量为0.5C | |
| D. | 在线圈进入磁场的过程中,作用力F与时间t的关系式为F=1.5+0.2t(N) |

 如图所示,半径R=1m的$\frac{1}{4}$圆弧导轨与水平面相接,从圆弧导轨顶端A,静止释放一个质量为m=20g的小木块,测得其滑至底端B时速度VB=3m/s,在圆弧轨道上克服摩擦力做功为0.11J(重力加速度g=10m/s2)
如图所示,半径R=1m的$\frac{1}{4}$圆弧导轨与水平面相接,从圆弧导轨顶端A,静止释放一个质量为m=20g的小木块,测得其滑至底端B时速度VB=3m/s,在圆弧轨道上克服摩擦力做功为0.11J(重力加速度g=10m/s2)