题目内容
8. 如图所示,质量分别为m1、m2的两个物块间用一轻弹簧连接,放在倾角为θ的光滑斜面上.平行于斜面、大小为F的拉力作用在m1上,使m1、m2一起向上作匀加速运动,斜面始终静止在水平地面上,则( )
如图所示,质量分别为m1、m2的两个物块间用一轻弹簧连接,放在倾角为θ的光滑斜面上.平行于斜面、大小为F的拉力作用在m1上,使m1、m2一起向上作匀加速运动,斜面始终静止在水平地面上,则( )| A. | 弹簧的弹力为$\frac{{m}_{2}}{{m}_{1}+{m}_{2}}$F | B. | 弹簧的弹力为$\frac{{m}_{1}}{{m}_{1}+{m}_{2}}$F | ||
| C. | 地面对斜面的摩擦力水平向左 | D. | 地面对斜面的摩擦力水平向右 |
分析 由题,m1、m2一起向上作匀加速运动,先根据牛顿第二定律求出加速度,再对m1研究,由牛顿第二定律求出弹簧的弹力.以斜面为研究对象,由平衡条件分析地面对斜面的摩擦力方向.
解答 解:A、B根据牛顿第二定律得:
对m1、m2整体:F-(m1+m2)gsinθ=(m1+m2)a,
对m2:F弹-m2gsinθ=m2a,
联立上两式得:F弹=$\frac{{m}_{2}}{{m}_{1}+{m}_{2}}F$.故A正确,B错误.
C、D以斜面为研究对象,分析受力情况:重力G、m1、m2的压力N1、地面的支持力N2,如图,
则由平衡条件可知,地面对斜面的摩擦力f2必定水平向左,斜面才能保持平衡.故C正确,D错误.
故选:AC
点评 本题解题关键是研究对象的选择,采用整体法和隔离法相结合的方法求解弹簧的弹力,运用隔离法分析,地面对斜面的摩擦力的方向.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
18.一物体受到几个共点的恒力作用而处于平衡状态,当撤去某个恒力后,物体不可能做( )
| A. | 匀加速直线运动 | B. | 匀减速直线运动 | C. | 匀变速曲线运动 | D. | 变加速曲线运动 |
19. 粗糙的水平面上有一个正方形线框,其边长为0.5m,质量为1.5kg,电阻为0.2Ω,线框与水平地面间的动摩擦因数μ=0.4.图中虚线区域内磁场的磁感应强度为0.4T.线框初始位置如图所示,受到拉力F作用后做初速为0,加速度为1m/s2的匀加速直线运动,等到线框左边刚进入磁场时,立即撤去F,结果线框右边滑到磁场的右边缘处速度刚好减为0,取g=10m/s2,则( )
粗糙的水平面上有一个正方形线框,其边长为0.5m,质量为1.5kg,电阻为0.2Ω,线框与水平地面间的动摩擦因数μ=0.4.图中虚线区域内磁场的磁感应强度为0.4T.线框初始位置如图所示,受到拉力F作用后做初速为0,加速度为1m/s2的匀加速直线运动,等到线框左边刚进入磁场时,立即撤去F,结果线框右边滑到磁场的右边缘处速度刚好减为0,取g=10m/s2,则( )
 粗糙的水平面上有一个正方形线框,其边长为0.5m,质量为1.5kg,电阻为0.2Ω,线框与水平地面间的动摩擦因数μ=0.4.图中虚线区域内磁场的磁感应强度为0.4T.线框初始位置如图所示,受到拉力F作用后做初速为0,加速度为1m/s2的匀加速直线运动,等到线框左边刚进入磁场时,立即撤去F,结果线框右边滑到磁场的右边缘处速度刚好减为0,取g=10m/s2,则( )
粗糙的水平面上有一个正方形线框,其边长为0.5m,质量为1.5kg,电阻为0.2Ω,线框与水平地面间的动摩擦因数μ=0.4.图中虚线区域内磁场的磁感应强度为0.4T.线框初始位置如图所示,受到拉力F作用后做初速为0,加速度为1m/s2的匀加速直线运动,等到线框左边刚进入磁场时,立即撤去F,结果线框右边滑到磁场的右边缘处速度刚好减为0,取g=10m/s2,则( )| A. | 线框运动的总时间为1.25s | |
| B. | 磁场区域的宽度d为0.625m | |
| C. | 从开始至线圈速度减为0的过程中,通过线圈横截面的电荷量为0.5C | |
| D. | 在线圈进入磁场的过程中,作用力F与时间t的关系式为F=1.5+0.2t(N) |
16.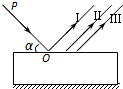 如图所示,一束由两种色光混合的复色光沿PO方向射向一上、下表面平行的厚玻璃平面镜的上表面,得到三束反射光束Ⅰ、Ⅱ、Ⅲ,平面镜的上下表面足够宽,则( )
如图所示,一束由两种色光混合的复色光沿PO方向射向一上、下表面平行的厚玻璃平面镜的上表面,得到三束反射光束Ⅰ、Ⅱ、Ⅲ,平面镜的上下表面足够宽,则( )
 如图所示,一束由两种色光混合的复色光沿PO方向射向一上、下表面平行的厚玻璃平面镜的上表面,得到三束反射光束Ⅰ、Ⅱ、Ⅲ,平面镜的上下表面足够宽,则( )
如图所示,一束由两种色光混合的复色光沿PO方向射向一上、下表面平行的厚玻璃平面镜的上表面,得到三束反射光束Ⅰ、Ⅱ、Ⅲ,平面镜的上下表面足够宽,则( )| A. | 光束Ⅰ仍为复色光,光束Ⅱ、Ⅲ为单色光,且玻璃对光束Ⅲ的折射率大于对光束Ⅱ的 | |
| B. | 改变α角,反射光束Ⅰ、Ⅱ、Ⅲ仍保持平行 | |
| C. | 增大α角且保持α≤90°,光束Ⅱ、Ⅲ会远离光束Ⅰ | |
| D. | 减小α角且保持α>0°,光束Ⅲ可能会从上表面消失 |
3.如图是甲、乙两物体做直线运动的v一t图象.下列表述正确的是( )


| A. | 甲乙都做匀变速直线运动 | B. | 0-1s内甲和乙的位移相等 | ||
| C. | 甲和乙的加速度方向相同 | D. | 甲的加速度比乙的小 |
17. 如图所示,两个小球A和B,中间用弹簧连接,并用细绳悬于天花板下,下面四对力中,属于相互作用力的是( )
如图所示,两个小球A和B,中间用弹簧连接,并用细绳悬于天花板下,下面四对力中,属于相互作用力的是( )
 如图所示,两个小球A和B,中间用弹簧连接,并用细绳悬于天花板下,下面四对力中,属于相互作用力的是( )
如图所示,两个小球A和B,中间用弹簧连接,并用细绳悬于天花板下,下面四对力中,属于相互作用力的是( )| A. | 绳对A的拉力和A对绳的拉力 | B. | 弹簧对A的拉力和绳对A的拉力 | ||
| C. | 弹簧对B的拉力和B受到的重力 | D. | B的重力和B对弹簧的拉力 |
11.下列作用在物体上的力能使物体做匀速直线运动的有( )
| A. | 3N,4N,8N | B. | 3N,5N,5N | C. | 2N,5N,10N | D. | 1N,7N,9N |
 如图所示,以10m/s匀速行驶的汽车即将通过路口,绿灯还有4s将熄灭,此时汽车距离停车线55m.该车加速时加速度大小为2m/s2,减速时加速度大小为5m/s2.此路段允许行驶的最大速度为15m/s.请计算说明:
如图所示,以10m/s匀速行驶的汽车即将通过路口,绿灯还有4s将熄灭,此时汽车距离停车线55m.该车加速时加速度大小为2m/s2,减速时加速度大小为5m/s2.此路段允许行驶的最大速度为15m/s.请计算说明: 轻绳的两端A、B固定在天花板上,绳能承受的最大拉力为120N.现用一粗糙挂钩将一重物挂在绳子上,结果挂钩停在C点,如图所示,两端与竖直方向的夹角分别为37°和53°.(sin 37°=0.6,cos 37°=0.8)求:
轻绳的两端A、B固定在天花板上,绳能承受的最大拉力为120N.现用一粗糙挂钩将一重物挂在绳子上,结果挂钩停在C点,如图所示,两端与竖直方向的夹角分别为37°和53°.(sin 37°=0.6,cos 37°=0.8)求: