题目内容
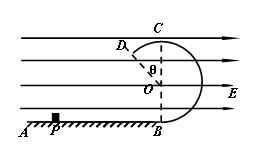
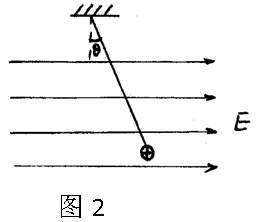
如图所示，在沿水平方向的匀强电场中有一固定点O，用一根长度为L=0.40m的绝缘细线把质量为m=0.20kg，带有正电荷的金属小球悬挂在O点，电荷量q = 0．5C小球静止在B点时，细线与竖直方向的夹角为θ=37°.现将小球拉至
位置A使细线水平后由
静止释放，求：
（1）匀强电场的场强大小；
（2）小球通过最低点C时细线对小球的拉力大小．
（取g = 10m／s2，sin37°=0.60，cos37°=0.80）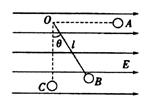
位置A使细线水平后由静止释放，求：（1）匀强电场的场强大小；
（2）小球通过最低点C时细线对小球的拉力大小．
（取g = 10m／s2，sin37°=0.60，cos37°=0.80）
（1）取小球为研究对象，静止时
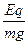= tanθ ①
解得：E=3N／C
②
(2）小球从A到C的运动过程由动能定理得：
mgL –EqL =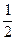
mv2 
③
到达最低点时竖直方向由牛顿第二定律得：
FT-mg = m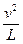
④
解得：FT =" 3mg-2qE" =" 3N " ⑤
评分标准：①③④每式2分，其余每式l分
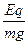= tanθ ①解得：E=3N／C
②(2）小球从A到C的运动过程由动能定理得：
mgL –EqL =
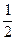mv2 ③到达最低点时竖直方向由牛顿第二定律得：
FT-mg = m
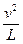④解得：FT =" 3mg-2qE" =" 3N " ⑤
评分标准：①③④每式2分，其余每式l分
略
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
名师点睛字词句段篇系列答案
相关题目
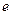=1．6×10
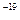C，质量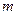
=0．91×10
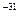kg，电子所受重力及电子之间的相互作用力均可忽略不计，不考虑相对论效应。
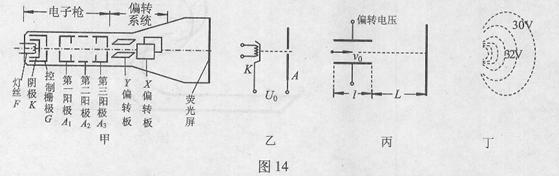（1）电子枪的三级加速可简化为如图14乙所示的加速电场，若从阴极逸出电子的初速度可忽略不计，要使电子被加速后的动能达到16×10
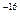J，求加速电压
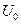为多大；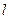
=4．0cm，两板间距离
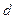=1．0cm，极板右端与荧光屏的距离
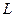=18cm，当在偏转电极上加
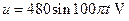的正弦交变电压时，如果电子进入偏转电场的初速度
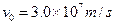，求电子打在荧光屏上产生亮线的最大长度；
、
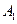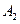和
三个阳极除了对电子加速外，还共同完成对电子的聚焦作用，其中聚焦电场可简化为如图14丁所示的电场，图中的虚线是该电场的等势线。请简要说明聚焦电场如何实现对电子的聚焦作用。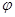
－x图线是一条与Ox轴重合的电场线上各点的电势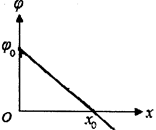
出时所用的时间为t/2.不计空气阻力.求:
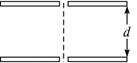
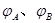的判断正确的是：
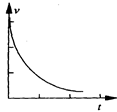
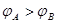D．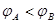
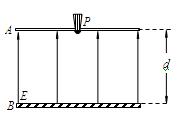
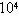m/s从板中逃逸出来，汇聚在第二块板上，如果每秒钟从板上每平方厘米上逃逸电子数n=
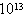个，电容器电容C=2.56×
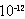F，极板面积S=1.82
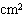，电子质量m=0.91×
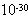kg，试问经过多少时间两极间的光电流停止？