题目内容
质量为m=0.5kg、可视为质点的小滑块，从光滑斜面上高h0=0.6m的A点由静止开始自由滑下。已知斜面AB与水平面BC在B处通过一小圆弧光滑连接。长为x0=0.5m的水平面BC与滑块之间的动摩擦因数μ=0.3，C点右侧有3级台阶（台阶编号如图所示），D点右侧是足够长的水平面。每级台阶的高度均为h=0.2m，宽均为L=0.4m。（设滑块从C点滑出后与地面或台阶碰撞后不再弹起）。
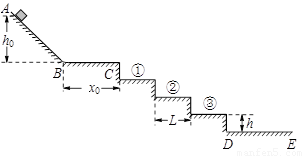
（1）求滑块经过B点时的速度vB；
（2）求滑块从B点运动到C点所经历的时间t；
（3）（辨析题）某同学是这样求滑块离开C点后，落点P与C点在水平方向距离x的：
滑块离开C点后做平抛运动，下落高度H=4h=0.8m，在求出滑块经过C点速度的基础上，根据平抛运动知识即可求出水平位移x。
你认为该同学解法是否正确？如果正确，请解出结果。如果不正确，请说明理由，并用正确的方法求出结果。
（1）
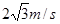；（2）0.155s；（3）见解析
【解析】(12分)（1）斜面AB上下滑，机械能守恒：
， （2分） 
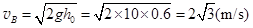（1分）
（2）动能定理：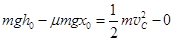
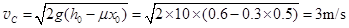， （1分）
（1分）
牛顿定律：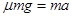
，
，
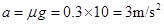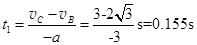（1分）
（1分）
（3）不正确，因为滑块可能落到某一个台阶上。正确解法： （1分）
假定无台阶，滑块直接落在地上，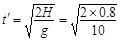
s=0.4s，水平位移
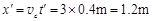，恰好等于3L（也就是恰好落在图中的D点），因此滑块会撞到台阶上。 （1分）
当滑块下落高度为2h时，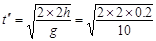
s=0.283s，水平位移
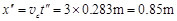，大于2L，所以也不会撞到第①、②台阶上，而只能落在第③级台阶上。 （1分）
则有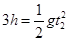
，
，
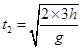（1分）
xPC
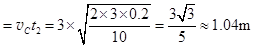（1分）
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
如图所示，水平桌面AB长L=1.5m，B端连接一个光滑斜面．使一个质量为m=0.5kg的小木块在F=1.5N的水平拉力作用下，从桌面上A端由静止开始向右运动，木块到达B端时撤去拉力F，木块由于惯性冲上斜面，而后又沿斜面滑下，最后停在AB的中点．忽略在连接处由于碰撞损失的能量，取g=10m/s2．求：
（2005?长宁区模拟）如图A、B是两个横截面积不同的竖直圆筒，其中各有一个活塞，它们距离筒底的高度均为h0=0.2m，质量分别为m1=1kg，m2=2kg，活塞下面盛有温度相同且不变的同种气体，活塞上面为真空，两个圆筒的底部是由细管相连通的．如果在A活塞上面再加放一个质量为m=0.5kg的物体，稳定后两活塞的高度差为
如图所示，固定在水平面上的横截面为“
”形的光滑长直导轨槽，槽口向上，槽内放置一金属滑块，滑块上有
”形槽的宽度略小．现有半径为r（r＜R）
如图是一种抛物器，轻质杠杆左端A是一个质量为M=10kg的重球，杠杆的右端是一个被抛的物体，质量为m=0.5kg，OA=OB=1m．此时杠杆与水平地面MN的夹角为θ=30°，要使其静止，则杆右端B应施加一个竖直向下的力F=
如图所示，质量为m=0.5kg的物体放在质量为M=4.5kg的平台上，随平台上、下做简谐运动．设在简谐运动过程中，二者始终保持相对静止．已知弹簧的劲度系数为k=400N/m，振幅为A=0.1m．试求：