题目内容
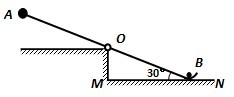
 如图是一种抛物器,轻质杠杆左端A是一个质量为M=10kg的重球,杠杆的右端是一个被抛的物体,质量为m=0.5kg,OA=OB=1m.此时杠杆与水平地面MN的夹角为θ=30°,要使其静止,则杆右端B应施加一个竖直向下的力F=
如图是一种抛物器,轻质杠杆左端A是一个质量为M=10kg的重球,杠杆的右端是一个被抛的物体,质量为m=0.5kg,OA=OB=1m.此时杠杆与水平地面MN的夹角为θ=30°,要使其静止,则杆右端B应施加一个竖直向下的力F=分析:利用杠杆平衡条件求所施加的力的大小,设抛出时,AB的速度都是v,根据机械能守恒定律求出v,根据竖直上抛运动的基本公式求解上升的高度即可求解.
解答:解:根据杠杆平衡条件得:
MglOA=(mg+F)lOB
带入数据解得:F=(M-m)g=95N
设抛出时,AB的速度都是v,变化的高度h=AOsin30°=0.5 m,根据机械能守恒得:
Mgh-mgh=
(M+m)v2.
v2=9.05
接着竖直上抛运动,上升的高度h1:
v2=2gh1
解得:h1=0.45 m
所以物体上升离地面MN的最大高度H=h+h1=0.95 m.
故答案为:95;0.95
MglOA=(mg+F)lOB
带入数据解得:F=(M-m)g=95N
设抛出时,AB的速度都是v,变化的高度h=AOsin30°=0.5 m,根据机械能守恒得:
Mgh-mgh=
| 1 |
| 2 |
v2=9.05
接着竖直上抛运动,上升的高度h1:
v2=2gh1
解得:h1=0.45 m
所以物体上升离地面MN的最大高度H=h+h1=0.95 m.
故答案为:95;0.95
点评:本题主要考查了杠杆平衡条件、机械能守恒定律及运动学基本公式的应用,难度适中.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目